Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
LQ
Những câu hỏi liên quan
Cho ΔABC với góc A = 60 độ, bán kính đường tròn ngoại tiếp bằng 7/√3 và bán kính đường tròn nội tiếp là √3. Tính diện tích và chu vi của Δ
cho biết kết quả
Diện tích của tam giác là 10√3
Chu vi của tam giác là 20
Giúp mình với TT^TT
Giúp mk với:
Cho tam giác ABC với S là diện tích và p là nửa chu vi tam giác ABC. Gọi r là bán kính đường tròn nội tiếp góc A. CMR:\(r=\frac{S}{p}\)
Xét tam giác ABC có I là tâm đường tròn nội tiếp
\(\Rightarrow S_{ABC}=S_{AIB}+S_{BIC}+S_{CIA}=\frac{1}{2}AB.r+\frac{1}{2}BC.r+\frac{1}{2}CA.r\)
\(=\frac{1}{2}\left(AB+BC+CA\right).r=p.r\)
\(\Rightarrow r=\frac{S_{ABC}}{p}\)
Đúng 0
Bình luận (0)
cm nửa s tam giác= tích của nửa chu vi bán kính đường tròn nội tiếp trong tam giác đó
Cho tam giác ABC có chu vi bằng 30cm và diện tích bằng 45cm2. Vẽ đường tròn (O) nội tiếp ΔABC. Tính bán kính của đường tròn đó.
Gọi D, E, F lần lượt là tiếp điểm của (O) với BC, AC, AB
\(\Rightarrow OD\perp BC\) ; \(OE\perp AC\) ; \(OF\perp AB\)
Và \(OD=OE=OF=R\)
Ta có:
\(S_{ABC}=S_{OAB}+S_{OAC}+S_{OBC}\)
\(=\dfrac{1}{2}OF.AB+\dfrac{1}{2}OE.AC+\dfrac{1}{2}OD.BC\)
\(=\dfrac{1}{2}R.AB+\dfrac{1}{2}R.AC+\dfrac{1}{2}R.BC\)
\(=\dfrac{1}{2}R.\left(AB+AC+BC\right)\)
\(\Rightarrow45=\dfrac{1}{2}R.30\)
\(\Rightarrow R=3\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có chu vi bằng 30cm và diện tích bằng 45 c m 2 . Vẽ đường tròn (O) nội tiếp ΔABC. Bán kính của đường tròn đó bằng:
A.8cm
B.6 cm
C. 5 cm
D.3 cm
Gọi a,b,c là số đo 3 cạnh của tam giác ABC , r là bán kính đường tròn nội tiếp tam giác . Tính diện tích tam giác theo p và r, trong đó p là nửa chu vi tam giác
Chứng minh rằng nếu tam giác ABC có chu vi 2p, bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức : S = p.r
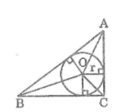
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : S A B C = S O A B + S O A C + S O B C
= (1/2).AB.r + (1/2).AC.r + (1/2).BC.r
= (1/2)(AB + AC + BC).r
Mà AB + AC + BC = 2p
Nên S A B C = (1/2).2p.r = p.r
Đúng 0
Bình luận (0)
Chứng minh rằng nếu tam giác ABC có chu vi 2p, bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức: S= p.r.
Ai giúp em với!!!
Gọi I,E,F lần lược là tiếp điểm của đường tròn tâm O nội tiếp với AB,BC,CA ta có OI = OE = OF = r
S ABC = S AOB + S BOC + S COA = AB.OI/2 + BC.OE/2 + CA.OF/2
= (AB + BC + CA).r/2 = pr
Đúng 0
Bình luận (0)
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : SABC = SOAB + SOAC + SOBC
\(=\left(\frac{1}{2}\right)AB.r+\left(\frac{1}{2}\right).AC.r+\left(\frac{1}{2}\right).BC.r\)
\(=\left(\frac{1}{2}\right)\left(AB+AC+BC\right).r\)
Mà AB + AC + BC = 2p
Nên \(S_{ABC}=\left(\frac{1}{2}\right).2p.r=p.r\)
một tam giác có số đo diện tích (cm2) bằng số do chu vi (cm). tính bán kính đường tròn nội tiếp


