GIÚP MÌNH GIẢI BÀI NÀY VỚI Ạ
ĐỀ : GIẢI CÁC HỆ PHƯƠNG TRÌNH SAU
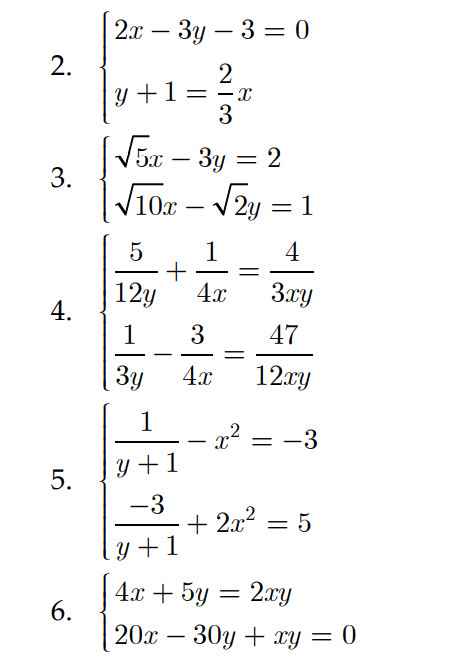
Giải giúp mình với ạ
Đề: giải các pt bậc hai 1 ẩn sau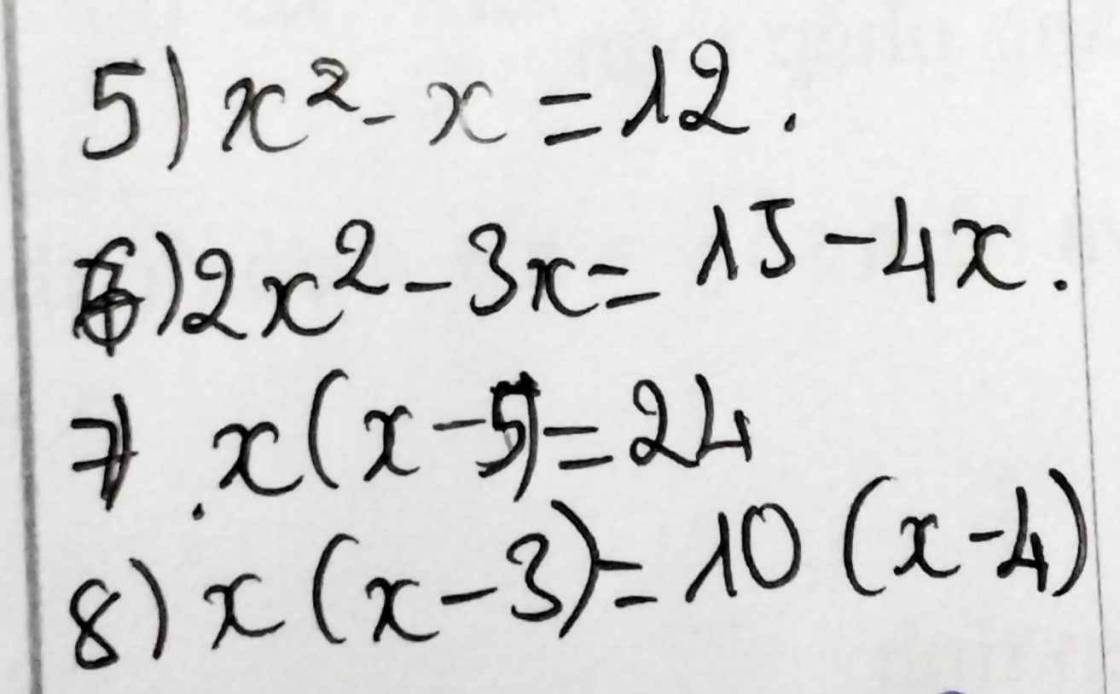
`x^2 -x=12`
`<=>x^2 -x-12=0`
`<=> x^2+3x-4x-12=0`
`<=> x(x+3)-4(x+3)=0`
`<=>(x+3)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
`---`
`2x^2-3x=15-4x`
`<=> 2x^2-3x+4x=15`
`<=>2x^2 +x-15=0`
`<=>2x^2+6x-5x-15=0`
`<=> 2x(x+3)-5(x+3)=0`
`<=>(x+3)(2x-5)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\2x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{5}{2}\end{matrix}\right.\)
`---`
`x(x-5)=24`
`<=> x^2 -5x-24=0`
`<=>x^2+3x-8x-24=0`
`<=>x(x+3) -8(x+3)=0`
`<=>(x+3)(x-8)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=8\end{matrix}\right.\)
`----`
`x(x-3)=10(x-4)`
`<=> x^2 -3x =10x -40`
`<=>x^2 -3x-10x +40=0`
`<=> x^2 -13x+40=0`
`<=>x^2-5x-8x+40=0`
`<=> x (x-5) - 8(x-5)=0`
`<=>(x-5)(x-8)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=8\end{matrix}\right.\)
5. \(x^2-x=12\Leftrightarrow x^2-x-12=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
6. \(2x^2-3x=15-4x\Leftrightarrow2x^2+x-15=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-3\end{matrix}\right.\)
7. \(x\left(x-5\right)=24\Leftrightarrow x^2-5x-24=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-3\end{matrix}\right.\)
8. \(x\left(x-3\right)=10\left(x-4\right)\Leftrightarrow x^2-3x=10x-40\)
\(\Leftrightarrow x^2-13x+40=0\Leftrightarrow\left[{}\begin{matrix}x=8\\x=5\end{matrix}\right.\)
Giúp mik vs mik cần gấp. Cảm ơn ạ
Đề bài: giải phương trình
`b)2x^2-5x+2=0`
`<=>2x^2-4x-x+2=0`
`<=>(x-2)(2x-1)=0`
`<=>[(x=2),(x=1/2):}`
`d)12x^2-53x+20=0`
`<=>12x^2-48x-5x+20=0`
`<=>(x-4)(12x-5)=0`
`<=>[(x=4),(x=5/12):}`
\(b,2x^2-5x+2=0\\ \Leftrightarrow2x^2-4x-x+2=0\\ \Leftrightarrow2x\left(x-2\right)-\left(x-2\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=2\end{matrix}\right.\\ d,12x^2-53x+20=0\\ \Leftrightarrow12x^2-48x-5x+20=0\\ \Leftrightarrow12x\left(x-4\right)-5\left(x-4\right)=0\\ \Leftrightarrow\left(12x-5\right)\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}12x-5=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{12}\\x=4\end{matrix}\right.\)
giúp mình giải hệ phương trình câu này với
`2x+5y=11(1)`
`2x-3y=0(2)`
Lấy (1) trừ (2)
`=>8y=11`
`<=>y=11/8`
`<=>x=(3y)/2=33/16`
a) Ta có: \(\left\{{}\begin{matrix}2x+5y=11\\2x-3y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=11\\2x-3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{11}{8}\\2x=3y=3\cdot\dfrac{11}{8}=\dfrac{33}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{33}{16}\\y=\dfrac{11}{8}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{33}{16}\\y=\dfrac{11}{8}\end{matrix}\right.\)
b) Ta có: \(\left\{{}\begin{matrix}4x+3y=6\\2x+y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\4x+2y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\2x+y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-2=4\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=6\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(3;-2)
`b)4x+3y=6(1)`
`2x+y=4<=>4x+2y=8(2)`
Lấy (1) trừ (2) ta có:
`y=-2`
`<=>x=(4-2y)/2=3`
GIẢI BẤT PHƯƠNG TRÌNH |x-1|+|2-x| > 3
CÁC BẠN GIÚP MÌNH GIẢI BÀI NÀY VỚI
Giải các phương trình giúp mình bài này vớii mình cảm ơn trước nha
\(9,PT\Leftrightarrow x-6=3x-7\left(x\ge6\right)\\ \Leftrightarrow x=\dfrac{1}{2}\left(ktm\right)\\ \Leftrightarrow x\in\varnothing\\ 10,PT\Leftrightarrow3x-2=4x^2-4x+1\left(x\le\dfrac{1}{2}\right)\\ \Leftrightarrow4x^2-7x+3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{4}\end{matrix}\right.\left(ktm\right)\Leftrightarrow x\in\varnothing\\ 11,PT\Leftrightarrow\sqrt{x^2+x-1}=2-x\left(x\le2\right)\\ \Leftrightarrow x^2+x-1=x^2-4x+4\\ \Leftrightarrow5x=5\Leftrightarrow x=1\left(tm\right)\\ 12,PT\Leftrightarrow\left(\sqrt{20-x}-4\right)+\left(\sqrt{x+5}-3\right)=0\left(5\le x\le20\right)\\ \Leftrightarrow\dfrac{4-x}{\sqrt{20-x}+4}+\dfrac{x-4}{\sqrt{x+5}+3}=0\\ \Leftrightarrow\left(x-4\right)\left(\dfrac{1}{\sqrt{x+5}+3}-\dfrac{1}{\sqrt{20-x}+4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\\dfrac{1}{\sqrt{x+5}+3}=\dfrac{1}{\sqrt{20-x}+4}\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{x+5}+3=\sqrt{20-x}+4\\ \Leftrightarrow\left(\sqrt{x+5}-4\right)-\left(\sqrt{20-x}-3\right)=0\\ \Leftrightarrow\dfrac{x-11}{\sqrt{x+5}+4}+\dfrac{x-11}{\sqrt{20-x}+3}=0\\ \Leftrightarrow\left(x-11\right)\left(\dfrac{1}{\sqrt{x+5}+4}+\dfrac{1}{\sqrt{20-x}+3}\right)=0\\ \Leftrightarrow x=11\left(\dfrac{1}{\sqrt{x+5}+4}+\dfrac{1}{\sqrt{20-x}+3}>0\right)\\ \text{Vậy PT có nghiệm }x\in\left\{4;11\right\}\)
\(13,PT\Leftrightarrow\sqrt{x-1}+\sqrt{3x-2}=\sqrt{5x+1}\left(x\ge-\dfrac{1}{5}\right)\\ \Leftrightarrow4x-3+2\sqrt{\left(x-1\right)\left(3x-2\right)}=5x+1\\ \Leftrightarrow x+4=2\sqrt{3x^2-5x+2}\\ \Leftrightarrow x^2+8x+16=12x^2-20x+8\\ \Leftrightarrow11x^2-28x-8=0\\ \Delta'=14^2+8\cdot11=284\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{14-2\sqrt{71}}{11}\\x=\dfrac{14+2\sqrt{71}}{11}\end{matrix}\right.\)
\(14,ĐK:x\ge-1\)
Đặt \(\sqrt{x+1}=a\ge0\)
\(PT\Leftrightarrow2\sqrt{a^2-1+2a}-a=4\\ \Leftrightarrow2\sqrt{a^2+2a-1}=a+4\\ \Leftrightarrow4a^2+8a-4=a^2+8a+16\\ \Leftrightarrow3a^2-20=0\\ \Leftrightarrow a^2=\dfrac{20}{3}\Leftrightarrow x+1=\dfrac{20}{3}\Leftrightarrow x=\dfrac{17}{3}\left(tm\right)\)
\(15,ĐK:-3\le x\le6\)
Đặt \(\sqrt{x+3}+\sqrt{6-x}=a\ge0\)
\(\Leftrightarrow\dfrac{a^2-9}{2}=\sqrt{\left(x+3\right)\left(6-x\right)}\\ PT\Leftrightarrow a-\dfrac{a^2-9}{2}=3\\ \Leftrightarrow2a-a^2+9=6\\ \Leftrightarrow a^2-2a-3=0\\ \Leftrightarrow a=3\left(a\ge0\right)\\ \Leftrightarrow\sqrt{x+3}+\sqrt{6-x}=3\\ \Leftrightarrow\sqrt{x+3}-3+\sqrt{6-x}=0\\ \Leftrightarrow\dfrac{x-6}{\sqrt{x+3}+3}-\dfrac{x-6}{\sqrt{6-x}}=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\left(tm\right)\\\dfrac{1}{\sqrt{x+3}+3}=\dfrac{1}{\sqrt{6-x}}\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{x+3}+3=\sqrt{6-x}\\ \Leftrightarrow\sqrt{x+3}-\left(\sqrt{6-x}-3\right)=0\\ \Leftrightarrow\dfrac{x+3}{\sqrt{x+3}}+\dfrac{x+3}{\sqrt{6-x}+3}=0\\ \Leftrightarrow x=-3\left(\dfrac{1}{\sqrt{x+3}}+\dfrac{1}{\sqrt{6-x}+3}>0\right)\\ \text{Vậy PT có nghiệm }x\in\left\{6;-3\right\}\)
\(16,\) Đặt \(\sqrt{x^2-6x+6}=a\ge0\)
\(PT\Leftrightarrow a^2+3=4a\\ \Leftrightarrow a^2-4a+3=0\\ \Leftrightarrow\left[{}\begin{matrix}a=1\\a=3\end{matrix}\right.\)
Với \(a=1\Leftrightarrow x^2-6x+5=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Với \(a=3\Leftrightarrow x^2-6x-3=0\Leftrightarrow\left[{}\begin{matrix}x=3+2\sqrt{3}\\x=3-2\sqrt{3}\end{matrix}\right.\)
Vậy PT có nghiệm \(x\in\left\{1;5;3+2\sqrt{3};3-2\sqrt{3}\right\}\)
Giải giúp mình bài này với:
Giải phương trình sau:\(\sqrt{x^2+4}-2\sqrt{x+2}=0\)
\(\sqrt{x^2+4}-2\sqrt{x+2}=0\)
\(\Leftrightarrow\sqrt{x^2+4}=2\sqrt{x+2}\)
\(\Leftrightarrow\sqrt{x^2+4}=\sqrt{4x+8}\)
\(\Leftrightarrow\sqrt{x^2+4}^2=\sqrt{4x+8}^2\)
\(\Leftrightarrow x^2+4=4x+8\)
\(\Leftrightarrow x^2-4x-4=0\)
\(\Delta=\left(-4\right)^2-4.1.\left(-4\right)=16+16=32\)
Vậy \(x_1=\frac{4+\sqrt{32}}{2}\);\(x_2=\frac{4-\sqrt{32}}{2}\)
P/S: Ko chắc
\(\sqrt{x^2+4}-2\sqrt{x+2}=0.\)
\(\Rightarrow\sqrt{x^2+4}=2\sqrt{x+2}\)
\(\Rightarrow x^2+4=2x+4\)
\(\Rightarrow x^2+4-2x-4=0.\)
\(\Rightarrow x^2-2x=0\)
\(\Rightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}}\)
Vậy .............
Study well
chuyên toán thcsKhông biết bình phương à
giải hệ phương trình này giúp mình vs
\(\left\{{}\begin{matrix}x+y=5\\\dfrac{3}{5}+\dfrac{2}{x-y}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=5\\\dfrac{2}{x-y}=\dfrac{12}{5}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+y=5\\6\left(x-y\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=5\\x-y=\dfrac{5}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{35}{6}\\y=x-\dfrac{5}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{35}{12}\\y=\dfrac{25}{12}\end{matrix}\right.\)
a. \(ZnCl_2+Zn^{2+}+2Cl^-\)
b. \(FeSO_4\rightarrow Fe^{2+}+SO_4^{2-}\)
c. \(Zn\left(NO_3\right)_2\rightarrow Zn^{2+}+2NO_3^-\)
d. \(MgCl_2\rightarrow Mg^{2+}+2Cl^-\)