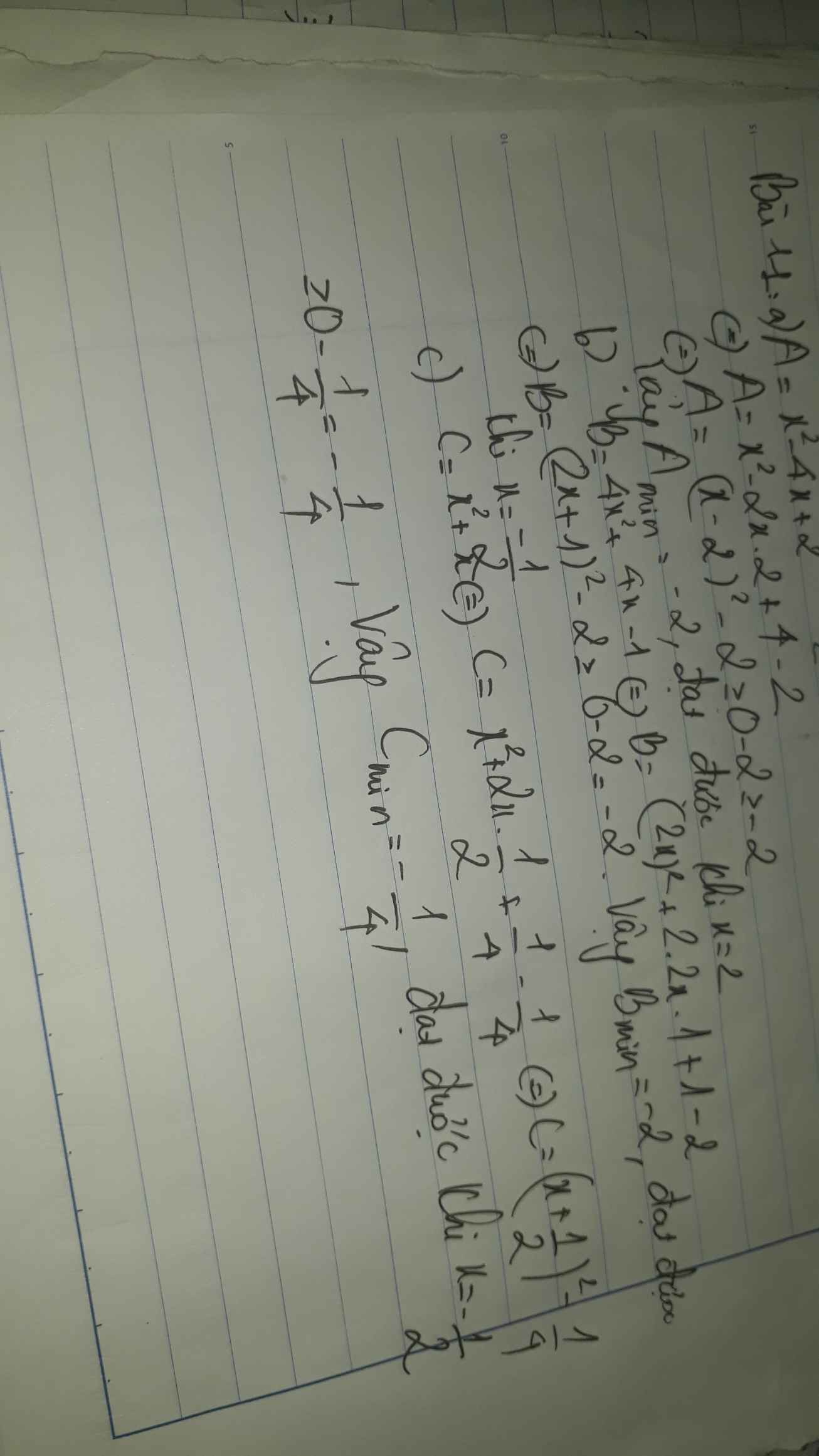ĐK: \(\hept{\begin{cases}-2\le x\le6\\-1\le x\le3\end{cases}}\Leftrightarrow-1\le x\le3\)

Thử bằng máy tính với \(x=-1;0;1;2;3\) thì thấy \(x=0\) thì A có giá trị nhỏ nhất so với các giá trị còn lại.

Từ đó ta có thể thử: 

Chứng minh \(A\ge A\left(3\right)\) hay \(A\ge\sqrt{3}\)

\(\Leftrightarrow\sqrt{-x^2+4x+12}\ge\sqrt{3}+\sqrt{-x^2+2x+3}\)

\(\Leftrightarrow-x^2+4x+12\ge3-x^2+2x+3+2\sqrt{3}\sqrt{-x^2+2x+3}\)

\(\Leftrightarrow x+3\ge\sqrt{3\left(-x^2+2x+3\right)}\)

\(\Leftrightarrow x^2+6x+9\ge-3x^2+6x+9\)(tương đương được vì \(x+3\ge-1+3>0\))

\(\Leftrightarrow4x^2\ge0\)

Do bđt cuối đúng nên bđt cần chứng minh là đúng.

Vậy Min A = 3 khi x = 0.

mình biết nội quy rồi nên đưng đăng nội quy

ai chơi bang bang 2 kết bạn với mình

mình có nick có 54k vàng đang góp mua pika 

ai kết bạn mình cho

a) Ta có: \(Q=-x^2-y^2+4x-4y+2=-\left(x^2+y^2-4x+4y-2\right)\)

\(=-\left(x^2-4x+4+y^2+4y+4\right)+10\)

\(=-\left[\left(x-2\right)^2+\left(y+2\right)^2\right]+10\le10\forall x,y\)

Vậy Max_Q=10 khi x=2, y=-2

b) +Ta có: \(A=-x^2-6x+5=-\left(x^2+6x-5\right)=-\left(x^2+6x+9-14\right)\)

\(=-\left(x^2+6x+9\right)+14=-\left(x+3\right)^2+14\le14\forall x\)

Vậy Max_A=14 khi x=-3

+Ta có: \(B=-4x^2-9y^2-4x+6y+3=-\left(4x^2+9y^2+4x-6y-3\right)\)

\(=-\left(4x^2+4x+1+9y^2-6y+1-5\right)\)

\(=-\left[\left(2x+1\right)^2+\left(3y-1\right)^2\right]+5\le5\forall x,y\)

Vậy Max_B=5 khi x=-1/2, y=1/3

c) Ta có: \(P=x^2+y^2-2x+6y+12=x^2-2x+1+y^2+6y+9+2\)

\(=\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\forall x,y\)

Vậy Min_P=2 khi x=1, y=-3

a) \(A=x^2-4x-2=\left(x^2-4x+4\right)-6=\left(x-2\right)^2-6\ge-6\left(\forall x\right)\)

Dấu "=" xảy ra khi: \(\left(x-2\right)^2=0\Rightarrow x=2\)

Vậy Min(A) = -6 khi x = 2

b) \(B=\left(x-1\right)\left(2x+3\right)-12\)

\(B=2x^2+x-3-12\)

\(B=2\left(x^2+\frac{x}{2}+\frac{1}{16}\right)-\frac{121}{8}\)

\(B=2\left(x+\frac{1}{4}\right)^2-\frac{121}{8}\ge-\frac{121}{8}\left(\forall x\right)\)

Dấu "=" xảy ra khi: \(2\left(x+\frac{1}{4}\right)^2=0\Rightarrow x=-\frac{1}{4}\)

Vậy \(Min_B=-\frac{121}{8}\Leftrightarrow x=-\frac{1}{4}\)

A = x² - 4x - 2

= ( x² - 4x + 4 ) - 6

= ( x - 2 )² - 6 ≥ -6 ∀ x

Đẳng thức xảy ra <=> x - 2 = 0 => x = 2

=> MinA = -6 <=> x = 2

B = ( x - 1 )( 2x + 3 ) - 12

= 2x² + x - 3 - 12

= 2x² + x - 15

= 2( x² + 1/2x + 1/16 ) - 121/8

= 2( x + 1/4 )² - 121/8 ≥ -121/8 ∀ x

Đẳng thức xảy ra <=> x + 1/4 = 0 => x = -1/4

=> MinB = -121/8 <=> x = -1/4

Ta có : \(A=x^2-4x-2\)

\(=\left[x^2-2\cdot x\cdot2+2^2\right]-6\)

\(=\left(x-2\right)^2-6\)

Vì \(\left(x-2\right)^2\ge0\forall x\)

=> \(\left(x-2\right)^2-6\ge-6\forall x\)

Dấu " = " xảy ra khi và chỉ khi (x - 2)² = 0 => x = 2

Vậy \(A_{min}=-6\)khi x = 2

\(B=\left(x-1\right)\left(2x+3\right)-12\)

\(B=x\left(2x+3\right)-1\left(2x+3\right)-12\)

\(B=2x^2+3x-2x-3-12\)

\(B=2x^2+x-15\)

\(B=2\left(x^2+\frac{1}{2}x-\frac{15}{2}\right)\)

\(B=2\left[x^2+2\cdot x\cdot\frac{1}{4}+\left(\frac{1}{4}\right)^2\right]-\frac{121}{8}\)

\(B=2\left(x+\frac{1}{4}\right)^2-\frac{121}{8}\)

Vì \(\left(x+\frac{1}{4}\right)^2\ge0\forall x\)

=> \(2\left(x+\frac{1}{4}\right)^2-\frac{121}{8}\ge-\frac{121}{8}\forall x\)

Dấu " = " xảy ra khi và chỉ khi (x + 1/4)² = 0 => x = -1/4

Vậy \(B_{min}=-\frac{121}{8}\)khi x = -1/4

bạn xem lại đề bài 1 là GTNN hay GTLN nha

1.

$x(x+2)(x+4)(x+6)+8$

$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$

$=a(a+8)+8$ (đặt $x^2+6x=a$)

$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$

Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$

2.

$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$

$=5-(x^2+5x-6)(x^2+5x+6)$

$=5-[(x^2+5x)^2-6^2]$

$=41-(x^2+5x)^2\leq 41$

Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$

3.

Đặt $x+3=a; 7-x=b$ thì $a+b=10$ 

$C=a^4+b^4$

Áp dụng BĐT Bunhiacopxky:

$(a^4+b^4)(1+1)\geq (a^2+b^2)^2$

$\Rightarrow C\geq \frac{(a^2+b^2)^2}{2}$
$(a^2+b^2)(1+1)\geq (a+b)^2=100$

$\Rightarrow a^2+b^2\geq 50$

$\Rightarrow C\geq \frac{50^2}{2}=1250$

Vậy $C_{\min}=1250$

Giá trị này đạt tại $a=b=5\Leftrightarrow x=2$