Có 2 người bắn cung (Ak là người thứ k bắn trúng k=1;2 ) biết rằng khả năng người thứ nhất bắn trúng là 0,6 và người thứ hai là 0,3 .tính xác xuất A:cả hai người trúng B:cả hai đều trượt C:có ít nhất 1 người trúng
ST
Những câu hỏi liên quan
Ba người cùng bắn vào một mục tiêu. Gọi Ak là sự kiện người thứ k bắn trúng mục tiêu, k 1 3, . Hãy viết bằng kí hiệu các sự kiện biểu thị rằng: a) Chỉ có người thứ nhất bắn trúng mục tiêu. b) Chỉ có 1 người bắn trúng mục tiêu. c) Chỉ có 2 người bắn trúng mục tiêu. d) Có ít nhất một người bắn trúng mục tiêu
Hai xạ thủ cùng bắn vào bia. Kí hiệu
A
K
là biến cố: Người thứ K bắn trúng, k 1, 2.a. Hãy biểu diễn các biến cố sau qua các biến cố
A
1
,
A
2
;A: Không ai bắn trúngB: Cả hai đều bắn trúngC: Có đúng một người bắn trúngD: Có ít nhất một người bắn trúngb. Chứng tỏ rằng
A
D
; B và C xung khắc nh...
Đọc tiếp
Hai xạ thủ cùng bắn vào bia. Kí hiệu A K là biến cố: "Người thứ K bắn trúng", k = 1, 2.
a. Hãy biểu diễn các biến cố sau qua các biến cố A 1 , A 2 ;
A: "Không ai bắn trúng"
B: "Cả hai đều bắn trúng"
C: "Có đúng một người bắn trúng"
D: "Có ít nhất một người bắn trúng"
b. Chứng tỏ rằng A = D ; B và C xung khắc nhau.
Ak là biến cố: "Người thứ k bắn trúng"
- A1 : "Người thứ nhất bắn trúng"
⇒ 
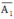: “Người thứ nhất không bắn trúng”.
- A2 : "Người thứ hai bắn trúng"
⇒ 
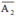: “Người thứ hai không bắn trúng”.
Đúng 0
Bình luận (0)
Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt là 0,8 ; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:
A.0.24.
B.0.96.
C. 0.46.
D.0.92
Gọi X là biến cố: “có đúng 2 người bắn trúng đích “
· Gọi A là biến cố: “người thứ nhất bắn trúng đích P(A)=0,8; P ( A ¯ ) = 0 , 2
Gọi B là biến cố: “người thứ hai bắn trúng đích P(B)=0,6; P ( B ¯ ) = 0 , 4
· Gọi C là biến cố: “người thứ ba bắn trúng đích P(C)=0,5; P ( C ¯ ) = 0 , 5
Ta thấy biến cố A, B, C là 3 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
P ( X ) = P ( A . B . C ¯ ) + P ( A . B ¯ . C ) + P ( A ¯ . B . C ) =0,8.0,6.0,5+0,8.0,4.0,5+0,2.0,6.0,5=0,46
Chọn C.
Đúng 0
Bình luận (0)
Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt là 0,8 ; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:
A. 0,24.
B. 0,96.
C. 0,46.
D. 0,92.
Gọi X là biến cố: “có đúng 2 người bắn trúng đích “
Gọi A là biến cố: “người thứ nhất bắn trúng đích” ⇒ P A = 0 , 8 ; P A ¯ = 0 , 2.
Gọi B là biến cố: “người thứ hai bắn trúng đích” ⇒ P B = 0 , 6 ; P B ¯ = 0 , 4.
Gọi C là biến cố: “người thứ ba bắn trúng đích” ⇒ P C = 0 , 5 ; P C ¯ = 0 , 5.
Ta thấy biến cố A, B, C là 3 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
P X = P A . B . C ¯ + P A . B ¯ . C + P A ¯ . B . C = 0 , 8.0 , 6.0 , 5 + 0 , 8.0 , 4.0 , 5 + 0 , 2.0 , 6.0 , 5 = 0 , 46.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Có ba xạ thủ đi săn đêm. Gọi
A
k
là biến cố:”xạ thủ thứ k bắn trúng đích” với k 1,2,3. Hãy dùng các phép toán nêu các biến cố biểu thị qua
A
1
,
A
2
,
A
3
.a) Biến cố M: “không có xạ thủ nào bắn trúng đích” A.
A
1
¯
∪
A
2...
Đọc tiếp
Có ba xạ thủ đi săn đêm. Gọi A k là biến cố:”xạ thủ thứ k bắn trúng đích” với k = 1,2,3. Hãy dùng các phép toán nêu các biến cố biểu thị qua A 1 , A 2 , A 3 .
a) Biến cố M: “không có xạ thủ nào bắn trúng đích”
A. A 1 ¯ ∪ A 2 ¯ ∪ A 3 ¯
B. A 1 ¯ ∪ A 2 ¯ ∪ A 3 ¯ h a y A 1 ¯ . A 2 ¯ . A 3 ¯
C. A 1 ¯ ∪ A 2 ¯ ∩ A 3 ¯ h a y A 1 ¯ ∪ A 2 ¯ A 3 ¯
D. A 1 ¯ ∩ A 2 ¯ ∪ A 3 ¯ h a y A 1 ¯ A 2 ¯ ∪ A 3 ¯
Theo bài ra biến cố Ak: “ xạ thủ thứ k bắn trúng đích ”, với k=1,2,3 thì biến cố đối
Biến cố M “ không có xạ thủ nào bắn trúng đích” , tức là cả ba xạ thủ đều bắn trượt nên :
Chọn B
Đúng 0
Bình luận (0)
Cả hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,7. Hãy tính xác suất để : Có ít nhất một người bắn trúng.
A. P(C) =0,95
B. P(C) = 0,97
C. P(C) = 0,94
D. P(C) = 0,96
Gọi C là biến cố "Có ít nhất một người bắn trúng bia", khi đó biến cố đối của B là biến cố C
Do đó
P
(
C
)
=
1
−
P
(
B
)
=
1
−
0
,
06
=
0
,
94
.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Hai xạ thủ cùng bắn vào bia. Kí hiệu A_K là biến cố : Người thứ k bắn trúng, k 1, 2
a) Hãy biểu diễn các biến cố dau qua các biến cố A_1,A_2
A: Không ai bắn trúng
B : Cả hai đều bắn trúng
C: Có đúng một người bắn trúng
D : Có ít nhất một người bắn trúng
b) Chứng tỏ rằng : Aoverline{D}; B và C xung khắc
Đọc tiếp
Hai xạ thủ cùng bắn vào bia. Kí hiệu \(A_K\) là biến cố : "Người thứ k bắn trúng", k = 1, 2
a) Hãy biểu diễn các biến cố dau qua các biến cố \(A_1,A_2\)
A: "Không ai bắn trúng"
B : " Cả hai đều bắn trúng"
C: " Có đúng một người bắn trúng"
D : " Có ít nhất một người bắn trúng"
b) Chứng tỏ rằng : \(A=\overline{D}\); B và C xung khắc
Phép thử T được xét là: "Hai xạ thủ cùng bắn vào bia".
Theo đề ra ta có = "Người thứ k không bắn trúng", k = 1, 2. Từ đó ta có:
a) A = "Không ai bắn trúng" = "Người thứ nhất không bắn trúng và người thứ hai không bắn trúng". Suy ra A = .
.
Tương tự, ta có B = "Cả hai đều bắn trúng" = .
.
Xét C = "Có đúng một người bắn trúng", ta có C là hợp của hai biến cố sau:
"Người thứ nhất bắn trúng và người thứ hai bắn trượt" = A1 . .
"Người thứ nhất bắn trượt và người thứ hai bắn trúng" = . A2 .
Suy ra C = A1 . ∪
. A2 .
Tương tự, ta có D = A1 ∪ A2 .
b) Gọi là biến cố: " Cả hai người đều bắn trượt". Ta có
=
.
= A.
Hiển nhiên B ∩ C = Φ nên suy ra B và C xung khắc với nhau.
Đúng 0
Bình luận (0)
Ba người cùng bắn vào một bia một cách độc lập. Xác suất để người thứ nhất, thứ hai, thứ ba bắn trúng đích lần lượt là 0,5; 0,6; và 0,8 Xác suất để có đúng 2 người bắn trúng đích là
A. 0,24
B. 0,46
C. 0,92
D. 0,96
Từ giả thiết suy ra xác suất để người thứ nhất, thứ hai, thứ ba bắn không trúng đích lần lượt là 0,5; 0,4 và 0,2
Để có đúng người bắn trúng đích thì có các trường hợp sau
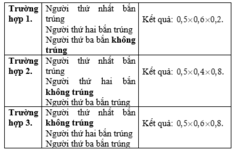
Vậy xác suất để có đúng người bắn trúng đích là
Chọn B.
Đúng 0
Bình luận (0)
Cả hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,7. Hãy tính xác suất để :Cả hai người cùng bắn trúng
A. P(A)= 0,75
B. P(A) = 0,6
C. P(A) = 0,56
D. P(A)=0,326
Gọi A 1 là biến cố “ Người thứ nhất bắn trúng bia”
A 2 là biến cố “ Người thứ hai bắn trúng bia”
Gọi A là biến cố “cả hai người bắng trúng”, suy ra A = A 1 ∩ A 2
Vì A 1 ; A 2 là độc lập nên P A = P A 1 P A 2 = 0 , 8 . 0 , 7 = 0 , 56
Chọn đáp án C.
Đúng 0
Bình luận (0)