Câu 22 ạ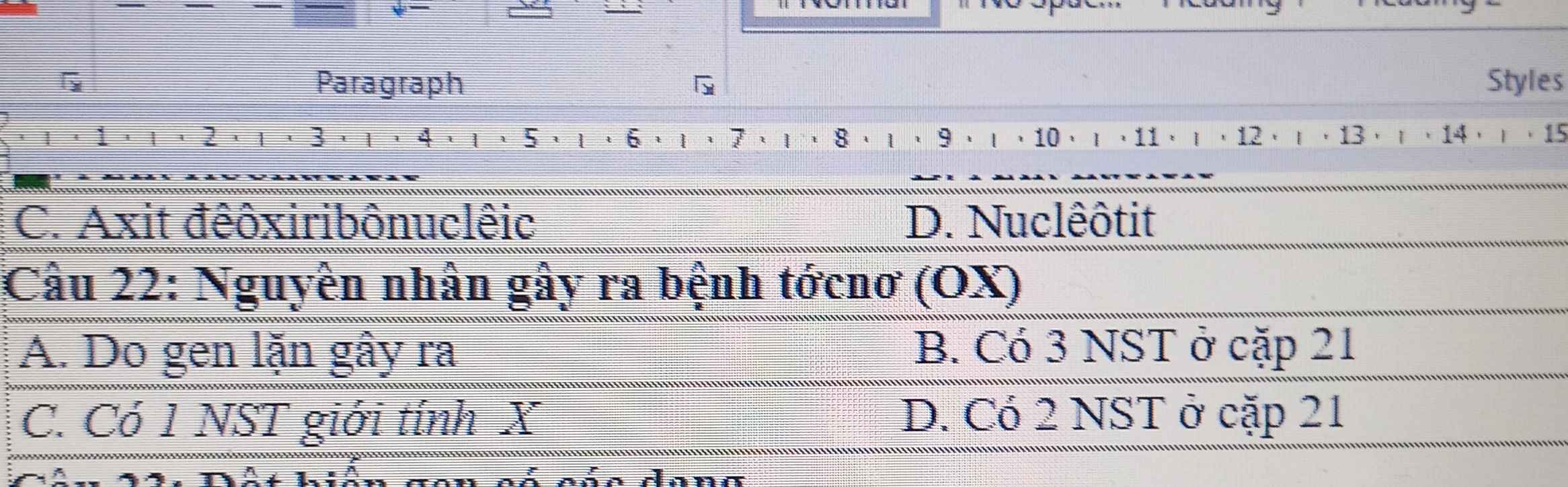
ND
Những câu hỏi liên quan
Giúp mình vs ạ Giúp câu 22 thoi ạ
GIÚP MÌNH CÂU 15 ĐẾN CÂU 22 Ạ!!
20A 21C 22B
Bạn chụp mặt trước nữa thì mình mới giúp được hết nha
Đúng 3
Bình luận (1)
Câu 22 làm sao ạ?
\(\overrightarrow{AB}=\left(2;0;2\right)=2\left(1;0;1\right)\Rightarrow\) mp trung trực AB nhận (1;0;1) là 1 vpt
Gọi M là trung điểm AB \(\Rightarrow M\left(2;0;0\right)\)
Pt mp trung trực AB:
\(1\left(x-2\right)+0\left(y-0\right)+1\left(z-0\right)=0\Rightarrow x+z-2=0\)
Đúng 0
Bình luận (0)
Giúp mình câu 22 nhé. Câu hỏi ở dưới ạ. :3
Xem chi tiết
\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{x+2017-\left(2015-x\right)}{\sqrt[3]{\left(x+2017\right)^2}+\sqrt[3]{\left(x+2017\right)\left(2015-x\right)}+\sqrt[3]{\left(2015-x\right)^2}}}{\dfrac{2000+x-\left(1998-x\right)}{\sqrt{2000+x}+\sqrt{1998-x}}}\)
\(=\lim\limits_{x\rightarrow-1}\dfrac{\sqrt{2000+x}+\sqrt{1998-x}}{\sqrt[3]{\left(x+2017\right)^2}+\sqrt[3]{\left(x+2017\right)\left(2015-x\right)}+\sqrt[3]{\left(2015-x\right)^2}}\)
\(=\dfrac{\sqrt{1999}+\sqrt{1999}}{\sqrt[3]{2016^2}+\sqrt[3]{2016^2}+\sqrt[3]{2016^2}}=\dfrac{2\sqrt{1999}}{3.24\sqrt[3]{294}}=\dfrac{\sqrt{1999}}{36\sqrt[3]{294}}\)
\(\Rightarrow a+b=1999+294\)
Đúng 2
Bình luận (0)
Giúp câu 22-30 vs ạ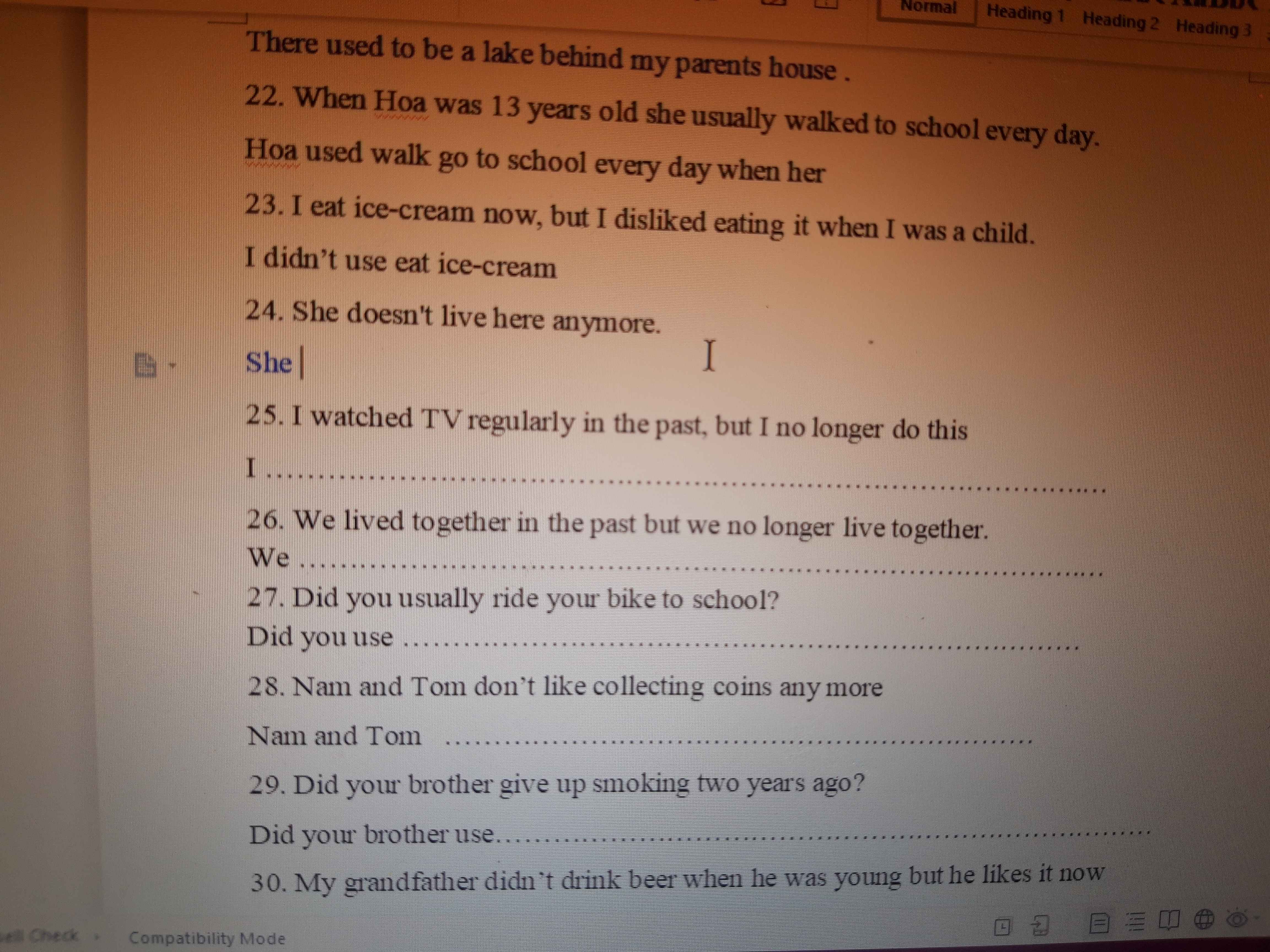
Giúp em câu 22 với ạ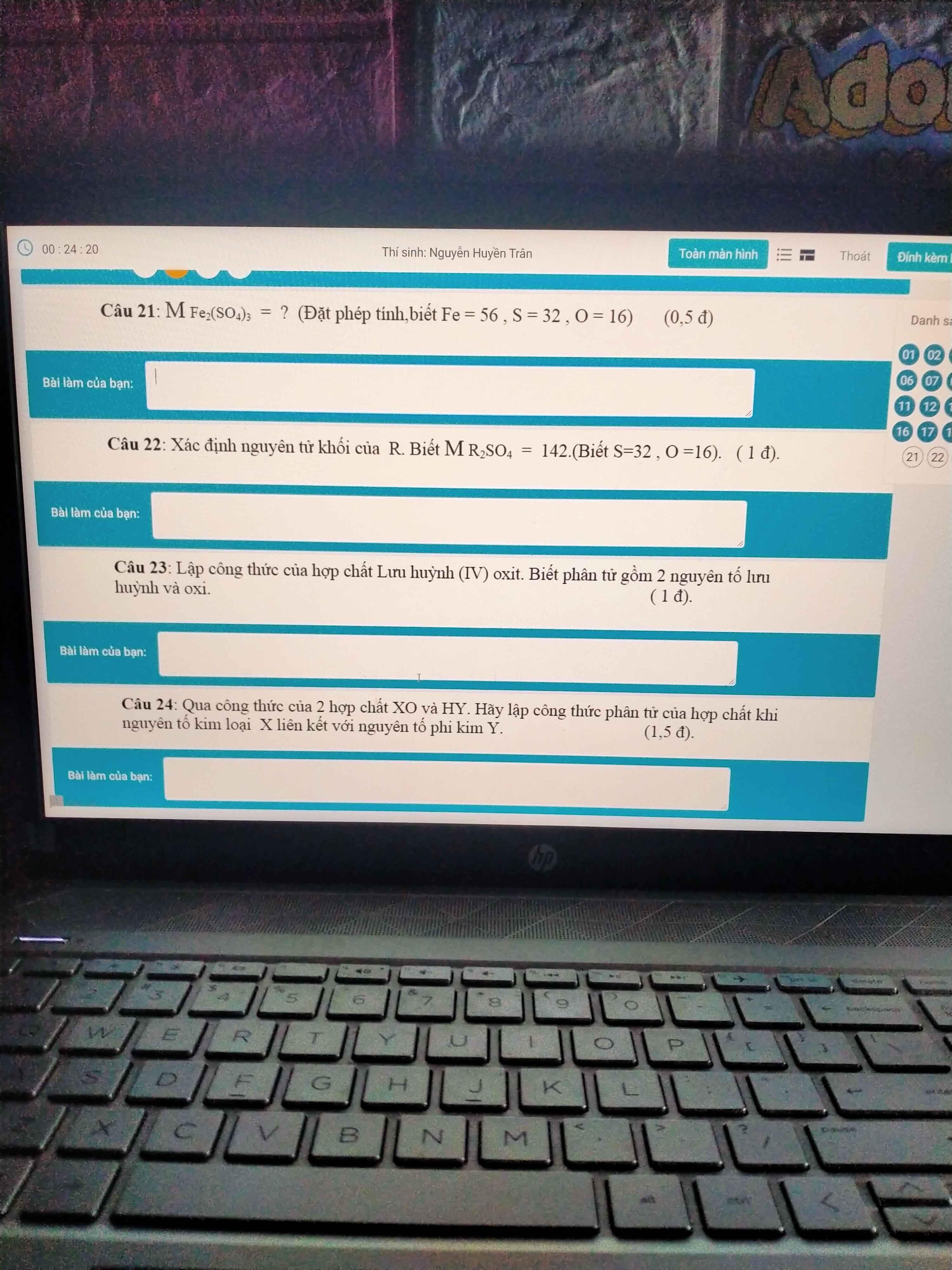
Câu 22 23 24 với ạ
Giải giúp e với ạ câu 22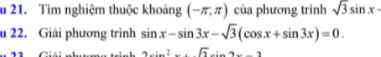
sinx - sin3x - \(\sqrt{3}\left(cosx+sin3x\right)=0\)
⇔ sinx - \(\sqrt{3}cosx-\left(1+\sqrt{3}\right)sin3x\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)-\left(1-\sqrt{3}\right)sin\left(\pi-3x\right)\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin\left(3x-\pi\right)=0\)
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin3\left(x-\dfrac{\pi}{3}\right)=0\)
Đặt a = x - \(\dfrac{\pi}{3}\) ta có phương trình mới
2sina + (1 - \(\sqrt{3}\))sin3a = 0 (1)
Sử dụng công thức sin3a = 3sina - 4sin3a đưa (1) về phương trình bậc 3 ẩn là a. Từ a suy ra x
Đúng 0
Bình luận (0)
Giải giúp e câu 22 vs ạ






