Tìm giá trị nhỏ nhất của biểu thức A=x+9/x khi x>0
NP
Những câu hỏi liên quan
1) Cho biểu thức A dfrac{x+sqrt{x}+1}{sqrt{x}} ( x 0 ) a) Tính giá trị biểu thức A khi x 9b) Tìm x để A 3 c) Tìm giá trị nhỏ nhất của A 2) Cho biểu thức B dfrac{sqrt{x}-2}{sqrt{x}+1} (x ≥ 0; x ≠ 4; x ≠ 9) a) Tính giá trị biểu thức tại x 4 - 2sqrt{3}b) Tìm x để B có giá trị âmc) Tìm giá trị nhỏ nhất của B 3) Cho biểu thức C dfrac{2x+2sqrt{x}+2}{sqrt{x}} với x 0; x ≠ 1 a) Tìm x để C 7b) Tìm x để C 6 c) Tìm giá trị nhỏ nhất của C – sqrt{x} 4) Cho biểu thức D dfrac{2-5sqrt{x}}{sqrt{x}+3...
Đọc tiếp
![]() 1) Cho biểu thức A = \(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\) ( x > 0 )
1) Cho biểu thức A = \(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\) ( x > 0 )
a) Tính giá trị biểu thức A khi x = 9
b) Tìm x để A = 3
c) Tìm giá trị nhỏ nhất của A
2) Cho biểu thức B = \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\) (x ≥ 0; x ≠ 4; x ≠ 9)
a) Tính giá trị biểu thức tại x = 4 - \(2\sqrt{3}\)
b) Tìm x để B có giá trị âm
c) Tìm giá trị nhỏ nhất của B
3) Cho biểu thức C = \(\dfrac{2x+2\sqrt{x}+2}{\sqrt{x}}\) với x > 0; x ≠ 1
a) Tìm x để C = 7
b) Tìm x để C > 6
c) Tìm giá trị nhỏ nhất của C – \(\sqrt{x}\)
4) Cho biểu thức D = \(\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}\) với x > 0 ; x ≠ 1
a) Tính giá trị biểu thức D biết \(x^2\) - 8x - 9 = 0
b) Tìm x để D có giá trị là \(\dfrac{1}{2}\)
c) Tìm x để D có giá trị nguyên
5) Cho biểu thức E = \(\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\) với x ≥ 0 ; x ≠ 1 ; x ≠ 9
a) Tính giá trị biểu thức E tại x = 4 + \(2\sqrt{3}\)
b) Tìm điều kiện của x để E < 1
c) Tìm x nguyên để E có giá trị nguyên
Bài 5:
a: Thay \(x=4+2\sqrt{3}\) vào E, ta được:
\(E=\dfrac{\sqrt{3}+1-1}{\sqrt{3}+1-3}=\dfrac{\sqrt{3}}{\sqrt{3}-2}=-3-2\sqrt{3}\)
b: Để E<1 thì E-1<0
\(\Leftrightarrow\dfrac{\sqrt{x}-1-\sqrt{x}+3}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
hay x<9
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne1\end{matrix}\right.\)
c: Để E nguyên thì \(4⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{-2;1;2;4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;5;7\right\}\)
hay \(x\in\left\{16;25;49\right\}\)
Đúng 2
Bình luận (0)
Câu 2:
a) Ta có \(x=4-2\sqrt{3}\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}-2\right)^2}=\sqrt{3}-2\)
Thay \(x=\sqrt{3}-1\) vào \(B\), ta được
\(B=\dfrac{\sqrt{3}-1-2}{\sqrt{3}-1+1}=\dfrac{\sqrt{3}-3}{\sqrt{3}}=1-\sqrt{3}\)
b) Để \(B\) âm thì \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< 0\) mà \(\sqrt{x}+1\ge1>0\forall x\) \(\Rightarrow\sqrt{x}-2< 0\Rightarrow\sqrt{x}< 2\Rightarrow x< 4\)
c) Ta có \(B=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=1-\dfrac{3}{\sqrt{x}+1}\)
Với mọi \(x\ge0\) thì \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+1\ge1\Rightarrow\dfrac{3}{\sqrt{x}+1}\le3\Rightarrow B=1-\dfrac{3}{\sqrt{x}+1}\ge-2\)
Dấu "=" xảy ra khi \(\sqrt{x}+1=1\Leftrightarrow x=0\)
Vậy \(B_{min}=-2\) khi \(x=0\)
Đúng 2
Bình luận (0)
Cho hai biểu thức: P = (sqrt(x - 2))/(sqrt(x) - 3) và Q = √x 6√x + 3 √x-3 9-x √x+3 (với x>0; x#9) a) Tính giá trị của P khi x = 9 . b) Rút gọn Q. c) Tìm x để biểu thức A = P.Q đạt giá trị nhỏ nhất.
Cho biểu thức $A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}$ và $B=\dfrac{3 \sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{4 x+6}{x-9}$ với $x \geq 0, x \neq 9$
1. Tình giá trị của biểu thức $A$ khi $x=\dfrac{1}{9}$.
2. Rút gọn biểu thức $B$.
3. Tìm giá trị của $x$ để biểu thức $P=A: B$ đạt giá trị nhỏ nhất.
1. \(x=\frac{1}{9}\) thỏa mãn đk: \(x\ge0;x\ne9\)
Thay \(x=\frac{1}{9}\) vào A ta có:
\(A=\frac{\sqrt{\frac{1}{9}}+1}{\sqrt{\frac{1}{9}}-3}=-\frac{1}{2}\)
2. \(B=...\)
\(B=\frac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\frac{4x+6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{3x-9\sqrt{x}+x+3\sqrt{x}-4x-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
3. \(P=A:B=\frac{\sqrt{x}+1}{\sqrt{x}-3}:\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\frac{\sqrt{x}+3}{-6}\)
Vì \(\sqrt{x}+3\ge3\forall x\)\(\Rightarrow\frac{\sqrt{x}+3}{-6}\le\frac{3}{-6}=-\frac{1}{2}\)
hay \(P\le-\frac{1}{2}\)
Dấu "=" xảy ra <=> x=0
toán lớp 9 khó zậy em đọc k hỉu 1 phân số
a. Với giá trị nào của x thì biểu thức A 1001 − | x + 9 | có giá trị lớn nhất? a. Với giá trị nào của x thì biểu thức A 1001 − | x + 9 | có giá trị lớn nhất? Tìm giá trị đóa. Với giá trị nào của x thì biểu thức A 1001 − | x + 9 | có giá trị lớn nhất? Tìm giá trị đó. b. Với giá trị nào của y thì biểu thức B | y − 2 | + 34 có giá trị nhỏ nhất? Tìm giá trị đó.ai làm được tôi tick cho
Đọc tiếp
a. Với giá trị nào của x thì biểu thức A = 1001 − | x + 9 | có giá trị lớn nhất? a. Với giá trị nào của x thì biểu thức A = 1001 − | x + 9 | có giá trị lớn nhất? Tìm giá trị đó
a. Với giá trị nào của x thì biểu thức A = 1001 − | x + 9 | có giá trị lớn nhất? Tìm giá trị đó. b. Với giá trị nào của y thì biểu thức B = | y − 2 | + 34 có giá trị nhỏ nhất? Tìm giá trị đó.
ai làm được tôi tick cho
Thôi nhắn chả hiểu luôn
Chịu vì nhắn ko hiểu luôn
Cho biểu thức đại số M = 3 – (x – 1)2
a/ Tính giá trị biểu thức M khi x = –2; x = 0; x = 3.
b/ Tìm x để M = 6
c/ Tìm giá trị nhỏ nhất của biểu thức M
a: Khi x=-2 thì \(M=3-\left(-2-1\right)^2=3-9=-6\)
Khi x=0 thì \(M=3-\left(0-1\right)^2=2\)
Khi x=3 thì \(M=3-\left(3-1\right)^2=3-2^2=-1\)
b: Để M=6 thì \(3-\left(x-1\right)^2=6\)
\(\Leftrightarrow\left(x-1\right)^2=-3\)(loại)
c: \(M=-\left(x-1\right)^2+3\le3\forall x\)
Dấu '=' xảy ra khi x=1
Đúng 2
Bình luận (0)
a, Thay x=-2 vào M ta có:
\(M=3-\left(-2-1\right)^2=3-\left(-3\right)^2=3-9=-6\)
Thay x=0 vào M ta có:
\(M=3-\left(0-1\right)^2=3-\left(-1\right)^2=3-1=2\)
Thay x=3 vào M ta có:
\(M=3-\left(3-1\right)^2=3-2^2=3-4=-1\)
b, Để M=6 thì:
\(3-\left(x-1\right)^2=6\\ \Leftrightarrow\left(x-1\right)^2=-3\left(vô.lí\right)\)
c, Ta có: \(\left(x-1\right)^2\ge0\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x=1\)
\(\Rightarrow M=3-\left(x-1\right)^2\le3\)
Dấu "=" xảy ra \(\Leftrightarrow x=1\)
Vậy \(M_{max}=3\Leftrightarrow x=1\)
Đúng 2
Bình luận (0)
Chú ý rằng vì
x
+
a
2
≥
0
với mọi giá trị của x và
x
+
a
2
0
khi x -a nên
x
+
a
2
+
b
≥
0...
Đọc tiếp
Chú ý rằng vì x + a 2 ≥ 0 với mọi giá trị của x và x + a 2 = 0 khi x = -a nên x + a 2 + b ≥ 0 với mọi giá trị của x và x + a 2 + b = b khi x = -a .Áp dụng điều này giải các bài tập sau:
Rút gọn rồi tìm giá trị của x để biểu thức x 2 x - 2 . x 2 + 4 x - 4 + 3 có giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy.
Điều kiện x ≠ 2 và x ≠ 0
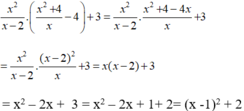
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.
Đúng 0
Bình luận (0)
Cho biểu thức : A= x-1/3x và B= ( x+1/2x-2 + 3x-1/x2 - 1 - x+3/2x+2) : 3/x+1 Với x # 0,x# -1,1.
a)Rút gọn biểu thức B
b)Tính giá trị của biểu thức A khi x thỏa mãn x2 - 2x = 0
c) tìm giá trị của x để B/A đạt giá trị nhỏ nhất .
b: \(A=\dfrac{2-1}{3\cdot2}=\dfrac{1}{6}\)
Đúng 0
Bình luận (0)
Bài 1: a)Tìm giá trị lớn nhất của biểu thức:
M = 2022 - |x - 9|
b)Tìm giá trị nhỏ nhất của biểu thức:
N = |x - 2021| - (- 2022)
a) \(M=2022-\left|x-9\right|\le2022\)
\(maxM=2022\Leftrightarrow x=9\)
b) \(N=\left|x-2021\right|+2022\ge2022\)
\(minN=2022\Leftrightarrow x=2021\)
Đúng 1
Bình luận (0)
Cho 2 biểu thức
A=(√x / √x-1 - 1/x-√x) : √x+1 / √x+2
B=√x /√x-3
x>0 ; x khác 1;x khác 9
a) tính giá trị biểu thức B khi x=36
b) tìm x để B<1/2
c) rút gọn A
d) tin giá trị x nguyên nhỏ nhất để P=A. B nguyên





