TÌm số nguyên n để biểu thức P= (n3-n2+2*n +7)/(n2+1) đạt giá trị là số nguyên
LH
Những câu hỏi liên quan
P=n3/6 + n2/2 + n/3 + (2n+1)/(1-2n) với n là số nguyên. tìm tất cả các số n để giá trị của P là một số nguyên
\(P=\dfrac{n^3+3n^2+2n}{6}+\dfrac{2n+1}{1-2n}\)
Vì n^3+3n^2+2n=n(n+1)(n+2) là tích của 3 số liên tiếp
nên n^3+3n^2+2n chia hết cho 3!=6
=>Để P nguyên thì 2n+1/1-2n nguyên
=>2n+1 chia hết cho 1-2n
=>2n+1 chia hết cho 2n-1
=>2n-1+2 chia hết cho 2n-1
=>\(2n-1\in\left\{1;-1;2;-2\right\}\)
=>\(n\in\left\{1;0;\dfrac{3}{2};-\dfrac{1}{2}\right\}\)
Đúng 2
Bình luận (0)
tìm n thuộc N để n3+n2-n+2 là số nguyên tố
H24
9 tháng 4 2021 lúc 12:43
Tìm số tự nhiên n để p là số nguyên tố biết : n3-n2+n-1
`P=n^3-n^2+n-1`
`=n^2(n-1)+(n-1)`
`=(n-1)(n^2+1)`
Vì n là stn thì p là snt khi
`n-1=1=>n=2`
Vậy n=2
Đúng 2
Bình luận (0)
MR
2 tháng 11 2021 lúc 9:57
Tìm Tìm số tự nhiên n để :
A=n3-n2+n-1 là số nguyên tố.
tìm số nguyên dương n để 3n2+5.n+2: n+1 có giá trị là số nguyên.
Tìm các số nguyên n để giá trị của biểu thức n 3 + 6 n 2 - 7 n + 4 chia hết cho giá trị của biểu thức n - 2.
Tìm các số nguyên n để giá trị của biểu thức n 3 + 6 n 2 - 7 n + 4 chia hết cho giá trị của biểu thức n - 2
Ở đây, ta có thực hiện đặt phép chia như câu 1 để tìm số dư và tìm điều kiện giá trị của n để thỏa mãn đề bài. Nhưng bài này ta làm cách biến đội như sau:
Đúng 0
Bình luận (0)
Tìm n ∈ N * sao cho : n3 – n2 + n – 1 là số nguyên tố
Ta có :
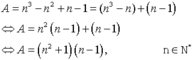
Nếu n = 1 suy ra A = 0
Nếu n = 2 suy ra A = 5 là số nguyên tố
Nếu n>2 thì A là tích của hai thừa số mà mỗi thừa số đều lớn hơn hai . Vậy A là hợp số
Vậy để A = n3 – n2 + n – 1 là số nguyên tố thì n = 2.
Đúng 0
Bình luận (0)
cho n là một số nguyên:
a) với giá trị nào của n thì \(\frac{4}{n2}\)là phân số
b) tìm các giá trị cả n để \(\frac{4}{n2}\) có giá trị là số nguyên
giúp mình hết sức có thể nha