Chứng minh rằng các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.
DT
Những câu hỏi liên quan
Dựa vào kết quả của bài 65, hãy chứng minh rằng: Các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.
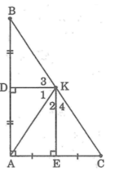
Kẻ đường trung trực của AC cắt BC tại K
Nối AK.
Ta có: KA = KC (tính chất đường trung trực)
Suy ra: Δ KAC cân tại K
Suy ra: ∠(KAC) = ∠C (1)
Lại có: ∠C + ∠B = 90o (t/chất tam giác vuông) (2)
Mà: ∠(KAC) + ∠(KAB) = ∠(BAC) = 90o (3)
Từ (1); (2) và (3) suy ra: ∠B = ∠(KAB)
Do đó; Δ KAB cân tại K ⇒ KA = KB
Suy ra: K thuộc đường trung trực của AB
Do đó K là giao điểm ba đường trung trực của Δ ABC
Suy ra: KB = KC = KA ⇒ K là trung điểm của BC
Vậy các đường trung trực của tam giác vuông đi qua trung điểm cạnh huyền
Đúng 0
Bình luận (0)
bài 1 cho tam giác ABC đường trung trục của ACD cắt Đường trung trục của BC tại O đường vuông góc với OA tại A cắt đường Vuông góc Với OB tại B ở D
cHỨNG minh rằng DO là đường phân giác của góc ADB
bài 2 chứng minh rằng các đường trung trực của tam giác vuông đi qua trung điểm cạnh huyền
Chứng minh các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền
CÁC BẠN ƠI GIÚP MÌNH VỚI NẾU VẼ ĐƯỢC HÌNH THÌ CÀNG TỐT
MÌNH XIN ĐƯỢC CẢM ƠN TRƯỚC
Đường trung trực cạnh nào bạn mà hình như đề bài của bạn sai rồi
Đúng 0
Bình luận (0)
Chứng minh rằng tâm của đường tròn đi qua 3 đỉnh của một tam giác vuông là trung điểm của cạnh huyền. Giúp mình nhanh với nha.
Vì tâm đường tròn đi qua 3 đỉnh của tam giác với mỗi tam giác chỉ có duy nhất 1 điểm.
Gọi I là trung điểm cạnh huyển BC của tam giác ABC vuông tại A.
Ta sẽ đi chứng minh I là tâm đường tròn đi qua 3 đỉnh tam giác ABC.
Thật vậy, trên tia đối tia IA , ta lấy điểm D sao cho IA=ID .
Vì I là trung điểm BC => IB=IC
Xét tam giác AIB và tam giác CID có:
AI=IC ; BI=ID ; AIB =CID (2 góc đối đỉnh)
=> Tam giác AIB =tam giác CID (c.g.c)
=> AB=CD; IAB = ICD
Vì IAB =ICD , mà 2 góc này ở vị trí so le trong
=> AB// CD Mà AB vuông góc với AC
=> CD vuông góc AC => ACD = 90
Xét tam giác BAC và DCA có:
AC chung ; AB=DC ; BAC = DCA =90
=> BAC = DCA(c.g.c)
=> BC = DA
Mà IB = IC = BC/2; AI=ID =DA/2
=> IB=IC=IA
=> I là tâm đường tròn đi qua A,B, C
Đúng 1
Bình luận (0)
CMR:Các đường trung trực của tam giác vuông đi qua trung điểm cạnh huyền của tam giác vuông
CAC BAN GIOI TOAN VAO DAY GIUP MINH NHA
CAC BAN GIAI HO MINH MINH SE LIKE CHO
Nối I với A,
Xét tam giác ABC vuông tại A, vẽ đường trung trực của AB và BC cắt ở I
\(\Rightarrow\)IA = IB \(\Rightarrow\)\(\Delta IAB\)cân tại I
\(\Rightarrow\)\(\widehat{IAB}=\widehat{IBA}\)
Mà \(\widehat{IAB}+\widehat{IAC}=\widehat{IAB}+\widehat{ICA}\left(=90^o\right)\)
\(\Rightarrow\)\(\widehat{IAC}=\widehat{ICA}\)
\(\Rightarrow\)\(\Delta IAC\)cân tại I \(\Rightarrow\)IA = IC
\(\Rightarrow\)I thuộc đường trung trực của đoạn thẳng AC
Vậy các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền
Đúng 0
Bình luận (0)
chứng minh rằng trong một tam giác ba chân đường cao, trung điểm các cạnh,trung điểm đoạn thẳng nối trực tâm của tam giác với các đỉnh cùng đi qua một đường tròn
cho tam giác ABC qua A kẻ đường thẳng xy bất kì không cắt các cạnh của tam giác ABC, kẻ BD, CE vuông góc với xy. Chứng minh rằng đường trung trực của đoạn thẳng DE luôn đi qua 1 điểm cố định
Cho tam giác ABC có AB=AC. Trên các cạnh AB và AC lấy các điểm D và E sao cho BD=CE. Gọi K là giao điểm của BE và CD.
a) Chứng minh rằng tam giác ADC = tam giác AEB
b) Chứng minh ba đường trung trực của tam giác ABC và trung trực của DE cùng đi qua một điểm
a: Xét ΔADC và ΔAEB có
AD=AE
góc A chung
AC=AB
=>ΔADC=ΔAEB
b: Gọi giao của 3 đường trung trực trong ΔABC là O
=>OB=OC
Kẻ OK vuông góc BC, OK cắt DE tại M
=>OK là trung trực của BC
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>OM vuông góc DE tạiM
Xét ΔOBD và ΔOCE có
OB=OC
góc OBD=góc OCE
BD=CE
=>ΔOBD=ΔOCE
=>OE=OD
=>OM là trung trực của DE
Đúng 0
Bình luận (0)
Chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.
bài 66 trang 49 sách bài tập toán lớp 7
Đúng 0
Bình luận (0)



