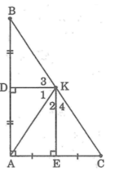
Kẻ đường trung trực của AC cắt BC tại K
Nối AK.
Ta có: KA = KC (tính chất đường trung trực)
Suy ra: Δ KAC cân tại K
Suy ra: ∠(KAC) = ∠C (1)
Lại có: ∠C + ∠B = 90o (t/chất tam giác vuông) (2)
Mà: ∠(KAC) + ∠(KAB) = ∠(BAC) = 90o (3)
Từ (1); (2) và (3) suy ra: ∠B = ∠(KAB)
Do đó; Δ KAB cân tại K ⇒ KA = KB
Suy ra: K thuộc đường trung trực của AB
Do đó K là giao điểm ba đường trung trực của Δ ABC
Suy ra: KB = KC = KA ⇒ K là trung điểm của BC
Vậy các đường trung trực của tam giác vuông đi qua trung điểm cạnh huyền