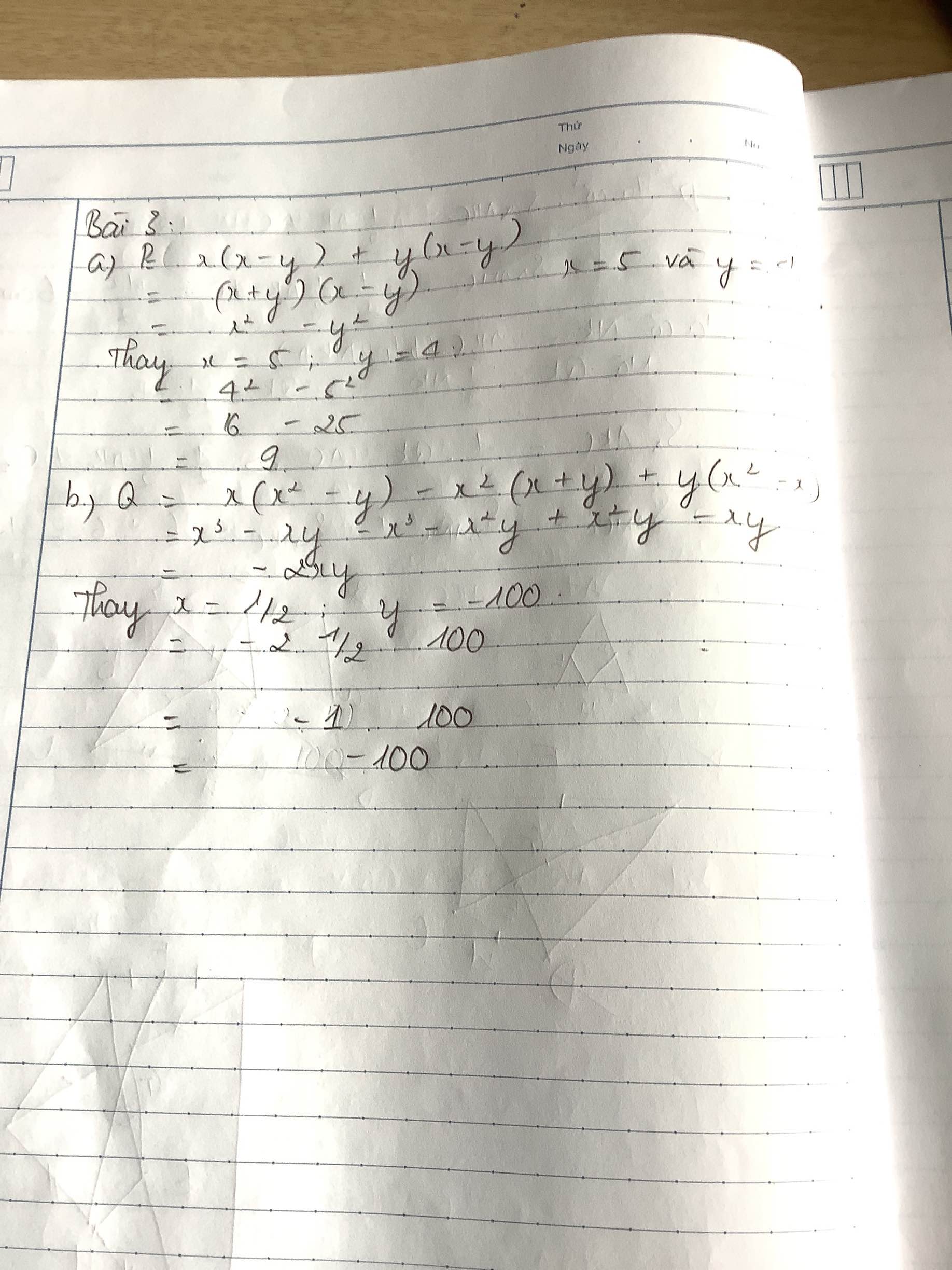a: Khi x=2 và y=-3 thì \(x^2+2y=2^2+2\cdot\left(-3\right)=4-6=-2\)

b: \(A=x^2+2xy+y^2=\left(x+y\right)^2\)

Khi x=4 và y=6 thì \(A=\left(4+6\right)^2=10^2=100\)

c: \(P=x^2-4xy+4y^2=\left(x-2y\right)^2\)

Khi x=1 và y=1/2 thì \(P=\left(1-2\cdot\dfrac{1}{2}\right)^2=\left(1-1\right)^2=0\)

Bài 1 : 

\(N=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)

Ta có : \(x+y+z=0\Rightarrow x+y=-z;y+z=-x;x+z=-y\)

hay \(-z.\left(-x\right)\left(-y\right)=-zxy\)

mà \(xyz=2\Rightarrow-xyz=-2\)

hay N nhận giá trị -2 

Bài 2 : 

\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)Đặt \(a=10k;b=3k\)

hay \(\frac{30k-6k}{10k-9k}=\frac{24k}{k}=24\)

hay biểu thức trên nhận giá trị là 24 

c, Ta có : \(a-b=3\Rightarrow a=3+b\)

hay \(\frac{3+b-8}{b-5}-\frac{4\left(3+b\right)-b}{3\left(3+b\right)+3}=\frac{-5+b}{b-5}-\frac{12+4b-b}{9+3b+3}\)

\(=\frac{-5+b}{b-5}-\frac{12+3b}{6+3b}\)quy đồng lên rút gọn, đơn giản rồi 

1.Ta có:\(x+y+z=0\)

\(\Rightarrow\hept{\begin{cases}x+y=-z\\y+z=-x\\x+z=-y\end{cases}}\)

\(\Rightarrow N=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\left(-x\right)\left(-y\right)=-2\)

2.Ta có:\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)

Đặt \(\frac{a}{10}=\frac{b}{3}=k\Rightarrow a=10k;b=3k\)

Ta có:\(A=\frac{3a-2b}{a-3b}=\frac{3.10k-2.3k}{10k-3.3k}=\frac{30k-6k}{10k-9k}=\frac{k\left(30-6\right)}{k\left(10-9\right)}=24\)

Vậy....

1. A = 6x^3 - 3x^2 + 2.|x| + 4 với x = -23

Thay x = -23 vào biểu thức trên, ta có:

A = 6.(-23)^3 - 3.(-23)^2 + 2.|-23| + 4

A = -74539

2. B = 2.|x| - 3.|y| với x = 12; y = -3

Thay x = 12; y = -3 vào biểu thức trên, ta có:

B = 2.|12| - 3.|-3|

B = 15

3. |2 + 3x| = |4x - 3|

ta có: 2 + 3x = \(\hept{\begin{cases}4x-3\Leftrightarrow4x-3\ge0\Leftrightarrow x\ge\frac{3}{4}\\-\left(4x-3\right)\Leftrightarrow4x-3< 0\Leftrightarrow x< \frac{3}{4}\end{cases}}\)

Nếu x >= 3/4, ta có phương trình:

2 + 3x = 4x - 3

<=> 3x - 4x = -3 - 2

<=> -x = 5

<=> x = 5 (TM)

Nếu x < 3/4, ta có phương trình:

 2 + 3x = -(4x - 3)

<=> 2 + 3x = -4x + 3

<=> 3x + 4x = 3 - 2

<=> 7x = 1

<=> x = 1/7 (TM) 

Vậy: tập nghiệm của phương trình là: S = {5; 1/7}

Ta có: H = x³ + x²y - xy² - y³ + x² - y² + 2x + 2y + 4 

= x²(x + y) - y²(x + y) + (x² - y²) + 2(x + y + 2)

= (x + y)(x² - y²) + (x² - y²) + 2(x + y + 1 + 1)

= (x + y + 1)(x² - y²) + 2(0 + 1)

= 0(x² - y²) + 2.1

= 2

Vậy H = 2

Chúc bn học tốt!

Help mik lẹ với ;-;

ta có : x=2,5 = 5/2  ;   y= 3/4

    Thay x= 5/2 ; y= 3/4 vào biểu thức 2x + 2xy - y, ta có

             2 . 5/2 + 2 . 5/2 . 3/4 - 3/4

           = 5 . 15/4 - 3/4

           = 75/4 - 3/4

           = 18

a) \(P=x\left(x-y\right)+y\left(x-y\right)=\left(x-y\right)\left(x+y\right)=x^2-y^2=5^2-4^2=9\)

b) \(Q=x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)=x^3-xy-x^3-x^2y+x^2y-xy=0\)

Bài 1:

$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$ 

$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$

$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$

Bài 2:
$8x^3-32y-32x^2y+8x=0$

$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$

$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$

$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)

$\Leftrightarrow x=4y$

Khi đó:

$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$

Bài cuối $x^21$ không rõ. Bạn xem lại.