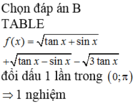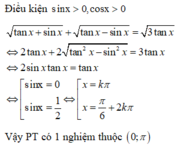Gải phương trình tanx = tan20°
H24
Những câu hỏi liên quan
Giải phương trình √3 tanx + 1 = 0 là phương trình bậc nhất đố với tanx.
√3tanx + 1 = 0 ⇔ tanx = (-√3)/3 ⇔ x = (-π)/6 + kπ, k ∈ Z)
Đúng 0
Bình luận (0)
Họ nghiệm của phương trình tan(x+frac{pi}{5})+ sqrt{3} 0 là?Phương trình tanx tanx/2 có họ nghiệm là?Nghiệm của phương trình √3 + 3tanx 0 có nghiệm là?Phương trình √3 + tanx 0 có nghiệm là?Họ nghiệm của phương trình tan2x - tanx 0 là?Phương trình lượng giác 3cotx - √3 0 có nghiệm là?Pt lượng giác 2cotx - √3 0 có nghiệm là?
Đọc tiếp
Họ nghiệm của phương trình tan(x+\(\frac{\pi}{5}\))+ \(\sqrt{3}\)= 0 là?
Phương trình tanx= tanx/2 có họ nghiệm là?
Nghiệm của phương trình √3 + 3tanx =0 có nghiệm là?
Phương trình √3 + tanx = 0 có nghiệm là?
Họ nghiệm của phương trình tan2x - tanx = 0 là?
Phương trình lượng giác 3cotx - √3 = 0 có nghiệm là?
Pt lượng giác 2cotx - √3 = 0 có nghiệm là?
Cho phương trình: 3/cos^2 x - 2× tanx + 1= 0. Đặt t= tanx ta được phương trình nào theo t
1+tan^2 x = 1/cos^2 x
=> 1+ t^2 = 1/cos^2 x
=> 3 + 3t^2 = 3/cos^2 x
PT TRỞ THÀNH :
3 + 3t^2 - 2t + 1 = 0
<=> 3t^2 - 2t + 4 = 0
Đúng 0
Bình luận (0)
Số nghiệm thuộc khoảng
0
;
π
của phương trình
tan
x
+
sin
x
+
tan
x
−
sin
x
3
tan
x
là. A. 0 B. 1. C. 2 D. 3
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x − sin x = 3 tan x là.
A. 0
B. 1.
C. 2
D. 3
Đáp án B
TABLE f ( x ) = tan x + sin x + tan x − sin x − 3 tan x đổi dấu 1 lần trong 0 ; π ⇒ 1 nghiệm
Đúng 0
Bình luận (0)
Số nghiệm thuộc khoảng
0
;
π
của phương trình
tan
x
+
sin
x
+
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1. C. 2. D. 3.
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1.
C. 2.
D. 3.
Số nghiệm thuộc khoảng
0
;
π
của phương trình.
tan
x
+
sin
x
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1 C. 2. D. 3.
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình. tan x + sin x = tan x - sin x = 3 tan x là
A. 0.
B. 1
C. 2.
D. 3.
Đáp án B
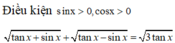
![]()
![]()
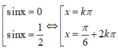
Vậy PT có 1 nghiệm thuộc (0; π )
Đúng 0
Bình luận (0)
Số nghiệm thuộc khoảng
0
;
π
của phương trình.
tan
x
+
sin
x
+
tan
x
-
sin
x
3
tan
x
là A. 0. B. 1 C. 2. D. 3
Đọc tiếp
Số nghiệm thuộc khoảng 0 ; π của phương trình.
tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1
C. 2.
D. 3
giải phương trình a.sinx + b.cosx = c bằng cách đưa về phương trình theo tanx/2
\(sinx=\dfrac{2tan\dfrac{x}{2}}{tan^2\dfrac{x}{2}+1}\)
\(cosx=\dfrac{1-tan^2\dfrac{x}{2}}{1+tan^2\dfrac{x}{2}}\)
Đặt \(t=tan\dfrac{x}{2}\)
Khi đó pt: \(\Rightarrow a\cdot\dfrac{2t}{t^2+1}+b\cdot\dfrac{1-t^2}{1+t^2}=c\)
\(\Rightarrow2t\cdot a+\left(1-t^2\right)\cdot b=\left(1+t^2\right)\cdot c\)
Đúng 0
Bình luận (0)
Giải phương trình:
\(Tan3x=Tanx\)
ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(tan3x=tanx\)
\(\Leftrightarrow3x=x+k\pi\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)
Đối chiếu điều kiện ta được \(x=k\pi\) là nghiệm của phương trình.
Đúng 0
Bình luận (0)