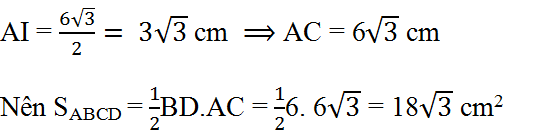tính diện tich hình thoi có cạnh dài 6cm và có 1 trong các góc là 60độ
H24
Những câu hỏi liên quan
Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60o.
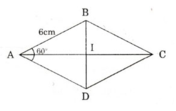
Cho hình thoi ABCD có cạnh AB = 6cm, góc ∠A = 60o.
- Cách 1:
ΔABD là tam giác đều nên BD = AB = 6cm
I là giao điểm của AC và BD => AI ⊥ DB
⇒ AI là đường cao của tam giác đều ABD nên
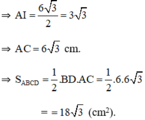
- Cách 2:
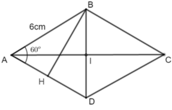
Khi đó ΔABD là tam giác đều. Từ B vẽ BH ⊥ AD thì HA = HD.
Nên tam giác vuông AHB là nửa tam giác đều.
BH là đường cao tam giác đều cạnh 6cm, nên
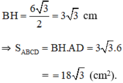
Đúng 0
Bình luận (0)
Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60o.
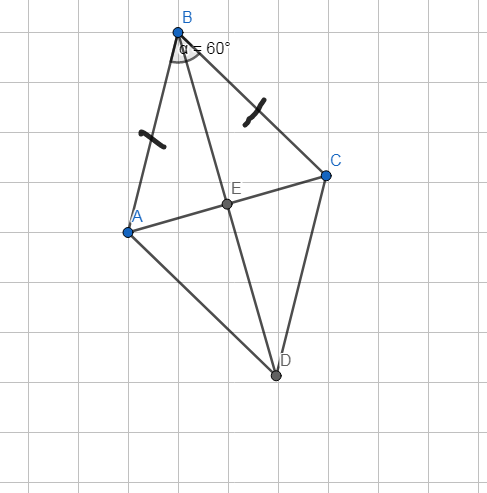
Ta có : AB=BC (ABCD là hình thoi)
=> Tam giác ABC cân tại B
Mà góc B =60o
=> Tam giác ABC đều.
=> AB=BC=CA=6cm
BD=2BE=2.\(\dfrac{\sqrt{3}}{2}\).6=6\(\sqrt{3}\)cm (bạn tự c/m nhé, nó không khó đâu).
SABCD=\(\dfrac{1}{2}\).6.6.\(\sqrt{3}\)=18\(\sqrt{3}\)
Đúng 0
Bình luận (0)
tính diện tích hình thoi biết cạnh của hình thoi là 6cm và một trong các góc của hình thoi có một góc bằng 30 độ
Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là \(60^0\) ?
Cho hình thoi ABCD có cạnh AB = 6cm, ∠A = 600

+ ABCD là hình thoi ⇒ ΔBAD cân tại A. Mà ∠A = 600 nên ΔABD là tam giác đều ⇒ BD = AB = 6cm
+ AC ⊥ BD và BI = ID = 3cm
Trong tam giác vuông AIB áp dụng định lý pitago
AI2 = AB2 – IB2 = 36 – 9 = 27 ⇒ AI = √27 (cm)
Suy ra: AC = 2AI = 2√27 (cm)
Vậy SABCD = 1/2AC.BD = 1/2.2√27 .6 = 12√27 (cm2)
Đúng 0
Bình luận (0)
ΔABD là tam giác đều nên BD = AB = 6cm
I là giao điểm của AC và BD => AI ⊥ DB
=> AI là đường cao của tam giác đều ABD nên
Đúng 0
Bình luận (0)
giải hộ mk bài này với
tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60 độ
Vào link sau tham khảo
Bài 35 Sgk tập 1 - trang 129 - Toán lớp 8 | Học trực tuyến
hk tốt!!!!!
Đúng 0
Bình luận (0)
1>tính diện tích một hình thang biết hai đáy có độ dài 5 cm và 7cm,một cạnh bên dài 6cm và tạo với đáy lớn góc có số đo bằng 30 độ
2>tính diện tích hình thoi có cạnh lầ 12 và có một góc là 30 độ
Tính chu vi và diện tích các hình sau:
a) Hình chữ nhật có chiều dài 18cm và chiều rộng 8cm
b) Hình vuông có cạnh 6cm
c) Hình thang cân có độ dài hai đáy là 4cm và 10cm, chiều cao 4cm, cạnh bên 5cm
d) Hình thoi có cạnh 5cm, độ dài hai đường chéo là 6cm và 8cm
e) Hình bình hành có độ dài hai cạnh là 10cm và 14cm, chiều cao 8cm
a) P= (18+8).2=52 (cm) ; S=18.8=144 (cm2)
b) P=6.4=24 (cm) ; S= 62=36 (cm2)
c) P=4+10+5+5=24 (cm) ; S= \(\dfrac{\left(4+10\right).4}{2}\)=28 (cm2)
d) P=5.4=20 (cm) ; S= \(\dfrac{6.8}{2}\)=24 (cm2)
e) P=(10+14).2=48 (cm2) ; S (chiều cao ứng với cạnh 10cm)=10.8=80cm2; S (chiều cao ứng với cạnh 14cm)=14.8=112cm2
Đúng 2
Bình luận (0)
Bài 1:Tính diện tích các hình sau:
a) Hình bình hành có độ dài một cạnh 15cm và chiều cao tương ứng là 6cm.
b) Hình thoi có dài 2 đường chéo là 4cm và 25dm.
c) Hình thang cân có độ dài hai cạnh đáy là 7m và 4m;chiều cao là 3,5m.
ko làm tắt nha mấy ní
a) Diện tích hình bình hành:
\(15.6=90\left(cm^2\right)\)
b) 25 dm = 250 cm
Diện tích hình thoi:
\(4\times250:2=500\left(cm^2\right)\)
c) Diện tích hình thang cân:
\(\left(7+4\right)\times3,5:2=19,25\left(m^2\right)\)
Đúng 0
Bình luận (0)
Câu 1: a) Tính diện tích hình thoi có độ dài hai đường chéo là 5cm và 7cm. b) Tính diện tích hình thang có độ dài hai đáy là 4cm và 6cm, đường cao 3cm c) Tính diện tích hình bình hành có độ dài đáy là 8cm và đường cao ứng với cạnh đáy đó là 7cm Câu 2: Viết tỉ số của cặp đoạn thẳng có độ dài như sau:AB 7cm và CD 14cm Câu 3: a) Cho D ABC ∽ D MNI. BiếtAˆA^ 800;NˆN^ 300. TínhCˆC^ b) Cho DABD DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho. Câu 4: Cho tam giác ABC có AB 4...
Đọc tiếp
Câu 1:
a) Tính diện tích hình thoi có độ dài hai đường chéo là 5cm và 7cm.
b) Tính diện tích hình thang có độ dài hai đáy là 4cm và 6cm, đường cao 3cm
c) Tính diện tích hình bình hành có độ dài đáy là 8cm và đường cao ứng với cạnh đáy đó là 7cm
Câu 2: Viết tỉ số của cặp đoạn thẳng có độ dài như sau:AB = 7cm và CD = 14cm
Câu 3: a) Cho D ABC ∽ D MNI. Biết
AˆA^
= 800;
NˆN^
= 300. Tính
CˆC^
b) Cho DABD DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho.
Câu 4: Cho tam giác ABC có AB = 4cm, BC = 6cm. Lấy M thuộc AB sao cho AM = 2cm. Lấy N thuộc AC sao cho AN = 3cm. Chứng minh MN // BC.
Câu 5: Cho tam giác ABC vuông tại A có AB = 12cm, AC = 15cm. Vẽ AM là tia phân giác của góc A (M thuộc BC). Biết BM = 8cm. Tính NC?
Câu 6 : Cho có AB = 3cm, AC = 4,5cm, BC = 6cm.
có DE= 12cm, EF=9cm, DF = 6cm. Chứng minh
.
Câu 7: a) Cho tam giác ABC có AB = 4cm, BC = 6cm. Lấy M thuộc AB sao cho AM = 2cm. Biết MN // BC. Tính MN?
b) Cho tam giác ABC có AB = 15cm, AC = 18cm. Trên AB lấy điểm M sao cho AM = 12cm, qua điểm M kẻ đoạn thẳng MN//BC. Tính độ dài đoạn thẳng AN?
Câu 8:Cho tam giác ABC có AB = 6cm, AC = 9cm. Trên cạnh AB lấy điểm M sao cho AM = 4cm. Kẻ MN song song với BC (NAC). Tính AN?
Câu 9 : H.thang ABCD(AB//CD) có AB = 6cm, CD = 24cm, BD = 12cm. Chứng minh: DABDDBDC.
Câu 10 : Cho nhọn. Trên cạnh Ox, đặt các đoạn thẳng OA = 6cm, OB = 18cm. Trên cạnh Oy, đặt các đoạn thẳng OC = 9cm, OD = 12cm.Chứng minh hai tam giác OAD và OCB đồng dạng.
Câu 11: Cho có
và
có MN = 6cm; MP = 8cm;
NP = 12cm. Hai tam giác ABC và MNP có đồng dạng không? Vì sao?
Câu 12: Cho góc nhọn xAy, trên tia Ax đặt hai đoạn thẳng AM = 10cm và AB = 12cm. Trên tia Ay đặt hai đoạn thẳng AN = 8cm và AC = 15cm. BN cắt CM tại H
Chứng minh đồng dạng với
Chứng minh
Câu 11:
Xét ΔABC và ΔMNP có
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}\left(=\dfrac{1}{2}\right)\)
Do đó: ΔABC~ΔMNP
Câu 12:
a: Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\left(\dfrac{10}{8}=\dfrac{15}{12}\right)\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC đồng dạng với ΔANB
b: Ta có: ΔAMC đồng dạng với ΔANB
=>\(\widehat{ACM}=\widehat{ABN}\)
Xét ΔHMB và ΔHNC có
\(\widehat{HBM}=\widehat{HCN}\)
\(\widehat{MHB}=\widehat{NHC}\)(hai góc đối đỉnh)
Do đó; ΔHMB đồng dạng với ΔHNC
=>\(\dfrac{HB}{HC}=\dfrac{BM}{CN}\)
=>\(HB\cdot CN=BM\cdot CH\)
Câu 10:
Xét ΔOAD và ΔOCB có
\(\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
góc O chung
Do đó: ΔOAD~ΔOCB
Đúng 0
Bình luận (0)