quy đồng các phân thức sau :
1) x/x-5 ; x+1
2) x/2x-8 ; x-1/4x-x^2
NT
Những câu hỏi liên quan
Quy đồng mẫu thức các phân thức sau
x
x
3
-
1
,
x
+
1
x
2
-
x
,
x
-
1
x
2
+
x
+
1
Đọc tiếp
Quy đồng mẫu thức các phân thức sau x x 3 - 1 , x + 1 x 2 - x , x - 1 x 2 + x + 1
quy đồng mẫu thức của các phân thức sau:
4x*2-3x+5/x*3-1 và 2x/x*2+x+1 ; 6/x-1
MTC : ( x - 1 )( x2 + x + 1 )
Ta có : \(\frac{4x^2-3x+5}{x^3-1}=\frac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{2x}{x^2+x+1}=\frac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{2x^2-2x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{6}{x-1}=\frac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{6x^2+6x+6}{\left(x-1\right)\left(x^2+x+1\right)}\)
Hnay mới học thì hnay trả lời nhá :P
\(\frac{4x^2-3x+5}{x^3-1};\frac{2x}{x^2+x+1}\)
Ta có : \(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
\(x^2+x+1=x^2+x+1\)
MTC : \(\left(x-1\right)\left(x^2+x+1\right)\)
\(\frac{4x^2-3x+5}{x^3-1}=\frac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{2x}{x^2+x+1}=\frac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{2x^2-2x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{2x}{x^2+x+1};\frac{6}{x-1}\)
Ta có : \(x^2+x+1=x^2+x+1\)
\(x-1=x-1\)
MTC : \(\left(x^2+x+1\right)\left(x-1\right)=x^3-1\)
\(\frac{2x}{x^2+x+1}=\frac{2x\left(x-1\right)}{\left(x^2+x+1\right)\left(x-1\right)}=\frac{2x^2-2x}{x^3-1}\)
\(\frac{6}{x-1}=\frac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{6x^2+6x+6}{x^3-1}\)
quy đồng mẫu thức các phân thức a) dfrac{1}{2x^3y}:dfrac{2}{3xy^2z^3}:dfrac{5}{4yz}b) dfrac{x+1}{10x^3-40x} và dfrac{5}{8x^3+16x^2}bài 2 áp dụng quy tắc đổi dấu hãy quy đồng mẫu thức các phân thứcdfrac{2-x}{3x-3x^2} và dfrac{x^2-2}{4x^5-4x^2}giúp mik với mik cần gấp
Đọc tiếp
quy đồng mẫu thức các phân thức a) \(\dfrac{1}{2x^3y}\):\(\dfrac{2}{3xy^2z^3}\):\(\dfrac{5}{4yz}\)
b) \(\dfrac{x+1}{10x^3-40x}\) và \(\dfrac{5}{8x^3+16x^2}\)
bài 2 áp dụng quy tắc đổi dấu hãy quy đồng mẫu thức các phân thức
\(\dfrac{2-x}{3x-3x^2}\) và \(\dfrac{x^2-2}{4x^5-4x^2}\)
giúp mik với mik cần gấp
quy đồng mẫu thức các phân thức a) dfrac{1}{2x^3y}: dfrac{2}{3xy^2z^3}:dfrac{5}{4yz}b) dfrac{x+1}{10x^3-40x} và dfrac{5}{8x^3+16x^2}bài 2 áp dụng quy tắc đổi dấu hãy quy đồng mẫu thức các phân thứcdfrac{2-x}{3x-3x^2} và dfrac{x^2-2}{4x^5-4x^2}
Đọc tiếp
quy đồng mẫu thức các phân thức a) \(\dfrac{1}{2x^3y}:\) \(\dfrac{2}{3xy^2z^3}\):\(\dfrac{5}{4yz}\)
b) \(\dfrac{x+1}{10x^3-40x}\) và \(\dfrac{5}{8x^3+16x^2}\)
bài 2 áp dụng quy tắc đổi dấu hãy quy đồng mẫu thức các phân thức
\(\dfrac{2-x}{3x-3x^2}\) và \(\dfrac{x^2-2}{4x^5-4x^2}\)
Bài 2:
a: \(\dfrac{1}{2x^3y}=\dfrac{6yz^3}{12x^3y^2z^3}\)
\(\dfrac{2}{3xy^2z^3}=\dfrac{2\cdot4x^2}{12x^3y^2z^3}=\dfrac{8x^2}{12x^3y^2z^3}\)
Đúng 0
Bình luận (0)
Quy đồng mẫu thức các phân thức sau:
4
x
-
x
2
x
x
+
3
;
x
-
3
3
x
x
+
1
Đọc tiếp
Quy đồng mẫu thức các phân thức sau: 4 x - x 2 x x + 3 ; x - 3 3 x x + 1
Mẫu thức chung: 3x(x + 3)(x + 1)
Ta có
Đúng 0
Bình luận (0)
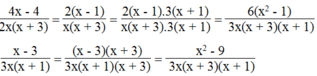
Quy đồng mẫu thức các phân thức sau 4 x 2 - 3 x + 5 x 3 - 1 ; 2 x x 2 + x + 1
M T 1 : x 3 – 1 = ( x - 1 ) ( x 2 + x + 1 )
M T 2 : x 2 + x + 1
⇒ M T C : ( x - 1 ) ( x 2 + x + 1 )
⇒ NTP1: 1
⇒ NTP2: x - 1
Quy đồng:
Đúng 0
Bình luận (0)
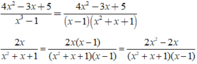
Quy đồng các phân thức sau:
9) \(\dfrac{2}{x^2-2x};\dfrac{x}{3x-6}\)
10) \(\dfrac{x}{x-5};x+1\)
11) \(\dfrac{x}{x^2+x+5};-3\)
12)\(\dfrac{x}{2x-8};\dfrac{x+1}{4x-x^2}\)
\(9,\dfrac{2}{x^2-2x}=\dfrac{6}{3x\left(x-2\right)};\dfrac{x}{3x-6}=\dfrac{x^2}{3x\left(x-2\right)}\\ 10,\dfrac{x}{x-5}=\dfrac{x}{x-5};x+1=\dfrac{\left(x+1\right)\left(x-5\right)}{x-5}\\ 11,-3=\dfrac{-3\left(x^2+x+5\right)}{x^2+x+5}\\ 12,\dfrac{x}{2x-8}=\dfrac{x^2}{2x\left(x-4\right)};\dfrac{x+1}{4x-x^2}=\dfrac{-2\left(x+1\right)}{2x\left(x-4\right)}\)
Đúng 0
Bình luận (0)
Quy đồng các phân thức sau
x-1/x^2+5X và x+1/ x^2-25
Tải Qanda về
\(\frac{x-1}{x^2+5x};\frac{x+1}{x^2-25}\)
ta có: \(\frac{x-1}{x^2+5x}=\frac{x-1}{x\left(x+5\right)}\)
\(\frac{x+1}{x^2-25}=\frac{x+1}{\left(x-5\right)\left(x+5\right)}\)
MTC: x(x-5).(x+5)
\(\frac{x-1}{x\left(x+5\right)_{\left(x-5\right)}}=\frac{\left(x-1\right)\left(x-5\right)}{x\left(x+5\right)\left(x-5\right)}=\frac{x^2-5x-x+5}{x\left(x+5\right)\left(x-5\right)}=\frac{x^2-4x+5}{x\left(x+5\right)\left(x-5\right)}\)
\(\frac{x+1}{\left(x-5\right)\left(x+5\right)_{\left(x\right)}}=\frac{x^2+x}{x\left(x-5\right)\left(x+5\right)}\)
Vậy ....
Quy đồng mẫu thức các phân thức sau:
1
6
x
3
y
2
;
x
+
1
9
x
2
y
4
;
x
-
1
4
x...
Đọc tiếp
Quy đồng mẫu thức các phân thức sau: 1 6 x 3 y 2 ; x + 1 9 x 2 y 4 ; x - 1 4 x y 3
