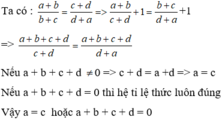chứng minh rằng nếu a+b/b+c=c+d/d+a (c+d khác 0) thì a=c hoặc a+b+c+d=0
1H
Những câu hỏi liên quan
Chứng minh rằng nếu \(\frac{a+b}{c+b}=\frac{c+d}{d+a}\)thì a=c hoặc a+b+c+d=0 ( với c,d khác 0)
Chứng minh rằng nếu a + b/ b+ c = c+ d/ d+ a thì a= c hoặc a+ b+ c+ d= 0 (với c+ d# 0)Cho x/a+2b+c= y/2a+y-z = z/4a-4b+c. Chứng minh rằng : a/x+2y+z=b/ 2x+y-z = c/ 4x- 4y+ c
Xem chi tiết
( với abc # 0 và các mẫu đều khác 0)
Chứng minh rằng : nếu a+b/b+c=c+d/c+a(c+d khác 0) thì a=c hoặc a+b+c+d=0
giải hộ mik nha
mik cần gấp
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{a+b}{b+c}=\frac{c+d}{c+a}=\frac{a+b+c+d}{a+b+c+d}\)
\(\Rightarrow\orbr{\begin{cases}a+b+c+d=0\\a=c\end{cases}}\)
Sửa đề:
Ta có: \(\frac{a+b}{b+c}=\frac{c+d}{d+a}\)
\(\Rightarrow\frac{a+b}{c+d}=\frac{c+b}{d+a}\)
\(\Rightarrow\frac{a+b}{c+d}+1=\frac{c+b}{d+a}+1\)
\(\Rightarrow\frac{a+b+c+d}{c+d}=\frac{c+d+b+d+c}{d+a}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{a+b+c+d}{c+d}=\frac{c+d+b+a}{d+a}=\frac{\left(a+b+c+d\right)-\left(c+d+b+c\right)}{\left(c+d\right)-\left(d+a\right)}=\frac{0}{\left(c+d\right)-\left(d+a\right)}=0\)
\(\Rightarrow\frac{a+b+c+d}{c+d}=0\)
Vì \(c+d\ne0\)
\(\Rightarrow a+b+c+d=0\left(đpcm\right)\)
và \(\frac{a+b+c+d}{c+d}-\frac{c+d+b+a}{d+a}=0\)
vd Thay a + b+ c= 1
ta có: \(\frac{1}{c+d}-\frac{1}{d+a}=0\)
\(\Rightarrow\frac{1}{c+d}=\frac{1}{d+a}\)
\(\Rightarrow d+a=c+d\)
\(\Rightarrow a=c\left(đpcm\right)\)
hok tốt!!
thank you 2b nha!!!
Chứng minh rằng nếu a+b/b+c =c+d/d+a (c+d khác 0) thì a=c và a+b+c+d=0
chứng minh rằng: nếu a/b=c/d khác 1 thì (a+b)/(a-b)=(c+d)/(c-d) với a,b,c,d khác 0
Đặt = t => a = bt ; c = dt thay vào từng vế
Đúng 0
Bình luận (0)
Đặt a/b=c/d= t suy ra a=bt; c=dt
(a+b)/(a-b)= bt+b/bt-b = b(t+1)/b(t-1)=t+1/t-1 (1)
(c+d)/(c-d)= dt+d/dt-d = d(t+1)/d(t-1)=t+1/t-1 (2)
Từ (1) và (2) suy ra (a+b)/(a-b)= (c+d)/(c-d)
Đúng 1
Bình luận (0)
Chứng minh rằng: Nếu a + b b + c = c + d d + a (c + d ≠ 0) thì a = c hoặc a = b + c + d = 0
Chứng minh rằng nếu:
(a + b + c + d) (a - b - c + d) = (a - b + c - d) (a + b - c - d)
thì\(\dfrac{a}{c}\)=\(\dfrac{b}{d}\)
(a, b, c, d khác 0)
Ta có: \(\left(a+b+c+d\right)\left(a-b-c+d\right)=\left(a-b+c-d\right)\left(a+b-c-d\right)\)
\(\Leftrightarrow\left(a+d\right)^2-\left(b+c\right)^2=\left(a-d\right)^2-\left(b-c\right)^2\)
\(\Leftrightarrow\left(a+d-a+d\right)\left(a+d+a-d\right)=\left(b+c-b+c\right)\left(b+c+b-c\right)\)
\(\Leftrightarrow2d\cdot2a=2c\cdot2b\)
\(\Leftrightarrow ad=bc\)
hay \(\dfrac{a}{c}=\dfrac{b}{d}\)
Đúng 1
Bình luận (0)
chứng minh rằng nếu a+b/c+d=b+c/d+a với a+b+c+d khác 0 thì a=c
\(\frac{a+b}{c+d}=\frac{b+c}{d+a}\)
<=>\(\frac{a+b}{c+d}+1=\frac{b+c}{d+a}+1\)
<=> \(\frac{a+b+c+d}{c+d}=\frac{a+b+c+d}{d+a}\)
<=> \(\frac{a+b+c+d}{c+d}-\frac{a+b+c+d}{d+a}=0\)
<=> \(\left(a+b+c+d\right)\left(\frac{1}{c+d}-\frac{1}{d+a}\right)=0\)
<=> \(\orbr{\begin{cases}a+b+c+d=0\\\frac{1}{c+d}-\frac{1}{d+a}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a+b+c+d=0\\c=a\end{cases}\left(đpcm\right)}}\)
Đúng 1
Bình luận (0)
Chứng minh rằng: Nếu a+c= 2b và 2bd=c(b+d) (b+d khác 0) thì a/b=c/d
\(2bd=c\left(b+d\right)\Rightarrow2b=\frac{c\left(b+d\right)}{d}\)
\(\Rightarrow a+c=\frac{c\left(b+d\right)}{d}\Rightarrow\frac{a+c}{c}=\frac{b+d}{d}\Rightarrow\frac{a}{c}+1=\frac{b}{d}+1\)
\(\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a}{b}=\frac{c}{d}\)
Ta có:
\(a+c=2b_{\left(1\right)}\)
\(2bd=c\left(b+d\right)_2\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow\)\(\left(a+c\right).d=c.\left(b+d\right)\)
\(\Rightarrow\)\(ad+cd=cb+cd\)( tính chất phân phối )
\(\Rightarrow\)\(ad=bc\)( rút gọn cả 2 vế cho \(cd\))
\(\Rightarrow\)\(\frac{a}{b}=\frac{c}{d}\)( tính chất cơ bản của tỉ lệ thức )
\(\Rightarrow\)\(\left(đpcm\right)\)