Giải hệ phương trình: x-12/4=y-9/3=z-1 và 3x+5y-z=2
TT
Những câu hỏi liên quan
TÌM NGHIỆM NGUYÊN CỦA HỆ PHƯƠNG TRÌNH1, hept{begin{cases}xyx+y+zxz2left(x-y+zright)yz3left(y-x+zright)end{cases}}TÌM NGHIỆM NGUYÊN DƯƠNG CỦA HỆ PHƯƠNG TRÌNH1, hept{begin{cases}x5y+3x11z+7end{cases}}(x, y, z nhỏ nhất)2,hept{begin{cases}x+2y+3z203x+5y+4z37end{cases}}(x, y, z nhỏ nhất)3, hept{begin{cases}z+yx+10yz10x+1end{cases}}4, hept{begin{cases}x+y+z1005x+3y+frac{z}{3}100end{cases}}GIẢI PHƯƠNG TRÌNH1, x^2-2x2sqrt{2x-1}2,frac{3x}{sqrt{3x+10}}sqrt{3x+1}-1MỌI NGƯỜI GIẢI GIÚP MÌNH VỚI
Đọc tiếp
TÌM NGHIỆM NGUYÊN CỦA HỆ PHƯƠNG TRÌNH
1, \(\hept{\begin{cases}xy=x+y+z\\xz=2\left(x-y+z\right)\\yz=3\left(y-x+z\right)\end{cases}}\)
TÌM NGHIỆM NGUYÊN DƯƠNG CỦA HỆ PHƯƠNG TRÌNH
1, \(\hept{\begin{cases}x=5y+3\\x=11z+7\end{cases}}\)(x, y, z nhỏ nhất)
2,\(\hept{\begin{cases}x+2y+3z=20\\3x+5y+4z=37\end{cases}}\)(x, y, z nhỏ nhất)
3, \(\hept{\begin{cases}z+y=x+10\\yz=10x+1\end{cases}}\)
4, \(\hept{\begin{cases}x+y+z=100\\5x+3y+\frac{z}{3}=100\end{cases}}\)
GIẢI PHƯƠNG TRÌNH
1, \(x^2-2x=2\sqrt{2x-1}\)
2,\(\frac{3x}{\sqrt{3x+10}}=\sqrt{3x+1}-1\)
MỌI NGƯỜI GIẢI GIÚP MÌNH VỚI
Ko biết sorry
ko bít sorry nhaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Giải phương trình :(y- 4,5 )^4 + (y-5,5 )^4 -1 = 0Tìm nghiệm nguyên của phương trình : 3x^2 + 5y^2 =345Rút gọn phân thức : (x^3 + y^3 -z^3-3xyz ) / (x+y)^2 + (y+z)^2 + (z+x)^2Cho x+y+z=0 . CMr x^3 + y^3 +z^3 =3xyza
Xem chi tiết
Giúp mk giải bài này vs @@ . Ai giải chi tiết mk sẽ tick cho <3 <3
giải hệ phương trình sau
\(\left\{{}\begin{matrix}x+\sqrt{y-2}+\sqrt{4-z}=y^2-5z+11\\y+\sqrt{z-2}+\sqrt{4-x}=z^2-5x+11\\z+\sqrt{x-2}+\sqrt{4-y}=x^2-5y+11\end{matrix}\right.\)
ĐKXĐ : \(2\le x,y,z\le4\)
Từ hệ phương trình ta suy ra được
\(\Sigma x+\Sigma\sqrt{x-2}+\Sigma\sqrt{4-x}=\Sigma x^2-5\Sigma x+33\\ \Leftrightarrow\Sigma\left(x^2-6x+9\right)+6=\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\\ \Leftrightarrow\Sigma\left(x-3\right)^2+6=\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\left(1\right)\)
Áp dụng bất đẳng thức \(\sqrt{A}+\sqrt{B}\le\sqrt{2\left(A+B\right)}\)
\(\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\le\Sigma\sqrt{2\left(x-2+4-x\right)}=\Sigma2=6\)
\(\Rightarrow\Sigma\left(x-3\right)^2+6\le6\Rightarrow\Sigma\left(x-3\right)^2\le0\)
Mà \(\Sigma\left(x-3\right)^2\ge0\)
\(\Rightarrow\left(x-3\right)^2=\left(y-3\right)^2=\left(z-3\right)^2=0\\ \Leftrightarrow x=y=z=3\)
Thay vào ta thấy thỏa mãn -> x=y=z=3 là nghiệm hpt
Đúng 2
Bình luận (0)
GIẢI GIÚP MÌNH BÀI TOÁN NÀY ĐI Ạ!Tìm nghiệm nguyên của hệ phương trìnhhept{begin{cases}xyx+y-zxz2left(x-y+zright)yz3left(y-x+zright)end{cases}} Tìm nghiệm nguyên dương của hệ phương trình hept{begin{cases}x5y+3x11z+7end{cases}}(x,y,z nhỏ nhất)hept{begin{cases}x+2y+3z203x+5y+4z37end{cases}}(x,y,z nhỏ nhất)
Đọc tiếp
GIẢI GIÚP MÌNH BÀI TOÁN NÀY ĐI Ạ!
Tìm nghiệm nguyên của hệ phương trình
\(\hept{\begin{cases}xy=x+y-z\\xz=2\left(x-y+z\right)\\yz=3\left(y-x+z\right)\end{cases}}\)
Tìm nghiệm nguyên dương của hệ phương trình
\(\hept{\begin{cases}x=5y+3\\x=11z+7\end{cases}}\)(x,y,z nhỏ nhất)
\(\hept{\begin{cases}x+2y+3z=20\\3x+5y+4z=37\end{cases}}\)(x,y,z nhỏ nhất)
Giải hệ phương trình sau:
a)\(\left\{{}\begin{matrix}\dfrac{x-12}{4}=\dfrac{y-9}{3}=z-1\\3x+5y-z=2\end{matrix}\right.\)
b)\(\left\{{}\begin{matrix}\dfrac{a+b}{6}=\dfrac{b+c}{7}=\dfrac{a+c}{8}\\a+b+c=14\end{matrix}\right.\)
Bạn coi lại câu b) đi nhé ( vì HPT chỉ có 1 dấu " = " thôi )
Đúng 0
Bình luận (0)
Câu 1: Giải phương trình và hệ phương trình sau:a) x^4+3x^2-40b) left{{}begin{matrix}x+2y5x-5y-9end{matrix}right.Câu 2: Trên mặt phẳng tọa độ Oxy cho điểm T (-2; -2), (P) có phương trình y-8x^2 và đường thẳng d có phương trình y - 2x - 6a) Điểm T có thuộc đường thẳng d không ?b) Xác định tọa độ giao điểm của đường thẳng d và (P)
Đọc tiếp
Câu 1: Giải phương trình và hệ phương trình sau:
a) \(x^4+3x^2-4=0\)
b) \(\left\{{}\begin{matrix}x+2y=5\\x-5y=-9\end{matrix}\right.\)
Câu 2: Trên mặt phẳng tọa độ Oxy cho điểm T (-2; -2), (P) có phương trình \(y=-8x^2\) và đường thẳng d có phương trình y = - 2x - 6
a) Điểm T có thuộc đường thẳng d không ?
b) Xác định tọa độ giao điểm của đường thẳng d và (P)
Câu 1:
a) Ta có: \(x^4+3x^2-4=0\)
\(\Leftrightarrow x^4+4x^2-x^2-4=0\)
\(\Leftrightarrow x^2\left(x^2+4\right)-\left(x^2+4\right)=0\)
\(\Leftrightarrow\left(x^2+4\right)\left(x^2-1\right)=0\)
mà \(x^2+4>0\forall x\)
nên \(x^2-1=0\)
\(\Leftrightarrow x^2=1\)
hay \(x\in\left\{1;-1\right\}\)
Vậy: S={1;-1}
Đúng 0
Bình luận (0)
Câu 1:
b) Ta có: \(\left\{{}\begin{matrix}x+2y=5\\x-5y=-9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7y=14\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=5-2y=1\end{matrix}\right.\)
Vậy: (x,y)=(1;2)
Đúng 0
Bình luận (0)
Câu 2:
a) Thay x=-2 vào (d), ta được:
\(y=-2\cdot\left(-2\right)-6=4-6=-2\)
Vậy: T(-2;-2) thuộc (d)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 0 và đường thẳng d có phương trình:
x
12
+
4
t
y
9
+
3
t
z...
Đọc tiếp
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Tìm giao điểm M của đường thẳng d và mặt phẳng α .
M ∈ d ⇒ M(12 + 4t; 9 +3t; 1 + t).
M ∈ α ⇒ 3.(12 + 4t) + 5.(9 + 3t) – (1 + t) – 2 = 0
⇔ 26t + 78 = 0.
⇔ t = -3.
⇒ M(0; 0; -2).
Đúng 0
Bình luận (0)
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 0 và đường thẳng d có phương trình:
x
12
+
4
t
y
9
+
3
t
z...
Đọc tiếp
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Viết phương trình mặt phẳng β chứa điểm M và vuông góc với đường thẳng d.
(β) vuông góc với d
⇒ (β) nhận vtcp của d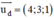 
là 1 vtpt.
(β) đi qua M(0; 0; -2)
⇒ (β): 4x + 3y + z + 2 = 0.
Đúng 0
Bình luận (0)
Tìm x, y, z
a,\(\frac{x}{y}=\frac{2}{3}\), \(\frac{x}{z}=\frac{4}{9}\)và\(^{x^3+y^3+z^3=-1009}\)
b,\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\)và x-2y+3z=14
c,3x=5y và \(x^2-y^2=4\)
d,2x=3y=5z và x+y-z=95
trình lời giải nữa nha, mình đang cần gấp!!