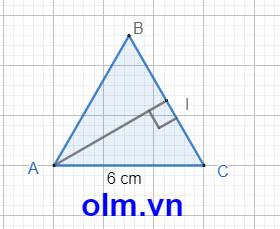
cho tam giác đều ABC có độ dài cạnh là 6cm kẻ AI vuông góc vs BC tính độ dài cạnh AI
HM
Những câu hỏi liên quan
cho tam giác abc độ dài cạnh là 6cm kẻ AI vuông góc với BC độ dài cạnh AI là
PB
31 tháng 12 2021 lúc 15:26
Cho tam giác đều ABC độ dài cạnh là 6cm. Kẻ AI vuông góc với BC. Độ dài cạnh AI là:
A. 3√3 cm
B. 3 cm
C. 3√2 cm
D. 6√3 cm
Cho tam giác đều ABC độ dài cạnh là 6cm. Kẻ AI vuông góc với BC. Độ dài cạnh AI là:
A. 3√3 cm
B. 3 cm
C. 3√2 cm
D. 6√3 cm
Đúng 1
Bình luận (1)
NT
26 tháng 6 2023 lúc 18:06
Câu 3: Cho tam giác đều ABC độ dài cạnh là 6cm. Kẻ AI vuông góc với BC. Độ dài cạnh AI là:
A. 3√3 cm
B. 3 cm
C. 3√2 cm
D. 6√3 cm
IC = \(\dfrac{1}{2}\)BC (vì trong tam giác đều đường cao cũng là trung tuyến, đường trung trực, đường phân giác của tam giác đó).
IC = 6 \(\times\) \(\dfrac{1}{2}\) = 3 (cm)
Xét \(\Delta\)AIC vuông tại C nên theo pytago ta có:
AI2 = AC2 - IC2 = 62 - 32 = 27 (cm)
AI = \(\sqrt{27}\) = 3\(\sqrt{3}\)(cm)
Chọn A. 3\(\sqrt{3}\)cm
Đúng 0
Bình luận (0)
Cho tam giác ABC cân ở A, gọi I là trung điểm của BC.
a/ Chứng minh : AI vuông góc vơi BC
b/ Cho AI = 6cm, BC = 8cm. Tính độ dài cạnh AB
c/ Từ I kẻ IM vuông góc với AB, IN vuông góc với AC. Chứng minh : IM = IN
d/ Chứng minh : MN song song với BC
a: Ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
b: Ta có: I là trung điểm của BC
nên IB=IC=4cm
Xét ΔAIB vuông tại I có
\(AB^2=AI^2+BI^2\)
hay \(AB=2\sqrt{13}\left(cm\right)\)
c: Xét ΔAMI vuông tại M và ΔANI vuông tại N có
AI chung
\(\widehat{MAI}=\widehat{NAI}\)
Do đó; ΔAMI=ΔANI
Suy ra; IM=IN
d: Xét ΔABC có
AM/AB=AN/AC
Do đó: MN//BC
Đúng 0
Bình luận (0)
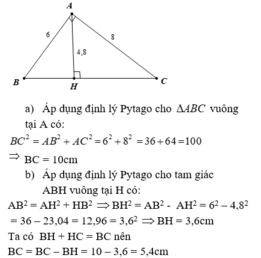
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. a) Tính độ dài cạnh BC. b)Kẻ AH vuông góc BC. Biết AH = 4,8cm. Tính độ dài các đoạn BH, CH .
Cho tam giác ABC vuông tại A có :AB=6cm; BC=8cm. BI là đường phân giác của góc B(I thuộc AC). Kẻ Ch vuông góc với đường thẳng BI (H thuộc BI)
a.Tính độ dài các cạnh AI,IC
b.C/m: Tam giác ABI đồng dạng với tam giác HCI,từ đó=>AB.CI=HC.BI
c. Tính diện tích HCI
a: Sửa đề: AC=8cm
BC=căn 6^2+8^2=10cm
Xét ΔBAC có BI là phân giác
nên AI/BA=CI/BC
=>AI/3=CI/5=(AI+CI)/(3+5)=8/8=1
=>AI=3cm; CI=5cm
b: Xét ΔABI vuông tại A và ΔHCI vuông tại H có
góc AIB=góc HIC
=>ΔABI đồng dạng với ΔHCI
=>AB/HC=BI/CI
=>AB*CI=BI*HC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm, BM là đường phân giác. Kẻ MK vuông góc với BC tại K.
a) Tính độ dài cạnh BC.
b) CM: AM=KM.
c) Kẻ AD vuông góc vs BC tại D. CM: Tia AK là tia phân giác của góc DAC.
d) CM: AB+AC<BC+AD.
bạn nào có lời giải bài này thì cho mk xin vs ạ :<
Cho tam giác vuông ABC vuông góc tại A. Có cạnh AB dài 6cm, cạnh AC dài 8cm. Tính độ dài cạnh BC.
\(\sqrt{6^2+8^2}=10\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác cân ABC có góc BAC = 120 độ. Vẽ đường cao AM (M thuộc BC)
a) Chứng minh rằng AM là tia phân giác của góc BAC
b) Kẻ MD vuông góc với AB ( D thuộc AB ), kẻ ME vuông góc vs AC ( E thuộc AC ) . Chứng minh tam giác ADE cân và DE // BC
c) Chứng minh rằng tam giác MDE đều
d) Đường vuông góc vs BC kẻ từ C cắt AB tại F . Tính độ dài cạnh AF biết CF = 6cm