Help please
tìm x,y trong hệ phương trình 15x -25y = 20y - 34x
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
giải hệ phương trình 17x - 10y = 48
15x - 25y = -96
Tìm x,y biết
1, 4x2 + 25y2 - 12x - 20y +13=0
2, 13x2 + y2 + 4xy - 34x - 2y +26=0
\(1,4x^2+25y^2-12x-20y+13=0\)
\(\Leftrightarrow\left(4x^2-12x+9\right)+\left(25y^2-20y+4\right)=0\)
\(\Leftrightarrow\left(2x-3\right)^2+\left(5y-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\5y-2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=3\\5y=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{2}{5}\end{matrix}\right.\)
1, \(4x^2+25y^2-12x-20y+13=0\)
\(\Leftrightarrow\left(4x^2-12x+9\right)+\left(25y^2-20y+4\right)=0\)
\(\Leftrightarrow\left(2x-3\right)^2+\left(5y-2\right)^2=0\)
Vì \(\left\{{}\begin{matrix}\left(2x-3\right)^2\ge0\\\left(5y-2\right)^2\ge0\end{matrix}\right.\Leftrightarrow\left(2x-3\right)^2+\left(5y-2\right)^2\ge0\)
Mà \(\left(2x-3\right)^2+\left(5y-2\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)^2=0\\\left(5y-2\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{2}{5}\end{matrix}\right.\)
Vậy...
b, \(13x^2+y^2+4xy-34x-2y+26=0\)
\(\Leftrightarrow\left(4x^2+y^2+1+4xy-4x-2y\right)+9x^2-30x+25=0\)
\(\Leftrightarrow\left(2x+y-1\right)^2+\left(3x-5\right)^2=0\)
Vì mỗi nhóm \(\ge0\) mà tổng 2 nhóm trên = 0
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x+y-1\right)^2=0\\\left(3y-5\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-7}{3}\\x=\dfrac{5}{3}\end{matrix}\right.\)
Vậy...
Cho hệ phương trình m x + y = 3 4 x + m y = 6 (m là tham số). Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x > 0 y > 1
A. – 2 < m < 4; m ≠ 2
B. – 2 < m < 4
C. m > −2; m ≠ 2
D. m < 4; m ≠ 2
Xét hệ
m x + y = 3 4 x + m y = 6 ⇔ y = 3 − m x 4 x + m 3 − m x = 6 ⇔ y = 3 − m x 4 x + 3 m − m 2 x = 6 ⇔ y = 3 − m x 4 − m 2 x = 6 − 3 m ⇔ y = 3 − m x 1 m 2 − 4 x = 3 m − 2 2
Hệ phương trình đã cho có nghiệm duy nhất ⇔ (2) có nghiệm duy nhất
m 2 – 4 ≠ 0 ⇔ m ≠ ± 2 ( * )
Khi đó hệ đã cho có nghiệm duy nhất
⇔ x = 3 m + 2 y = 3 − 3 m m + 2 ⇔ x = 3 m + 2 y = 6 m + 2
Ta có
x > 0 y > 2 ⇔ 3 m + 2 > 0 6 m + 2 > 1 ⇔ m + 2 > 0 4 − m m + 2 > 0 ⇔ m > − 2 4 − m > 0 ⇔ m > − 2 m < 4 ⇔ − 2 < m < 4
Kết hợp với (*) ta được giá trị m cần tìm là – 2 < m < 4; m ≠ 2
Đáp án: A
Cho hệ phương trình 2 3 x − 9 y + 6 x + y = 3 4 x − 3 y − 9 x + y = 1 y ≥ 0 ; x ≠ 3 y .
Nếu đặt 1 x − 3 y = a ; 1 x + y = b ta được hệ phương trình mới là:
A. 1 2 a + 1 6 b = 3 1 4 a − 1 9 b = 1
B. 2 a + 6 b = 3 4 a − 9 b = 1
C. 2 b + 6 a = 3 4 b − 9 a = 1
D. 2 3 a + 6 b = 3 4 a − 9 b = 1
Ta có 2 3 x − 9 y + 6 x + y = 3 4 x − 3 y − 9 x + y = 1 ⇔ 2 3 . 1 x − 3 y + 6. 1 x + y = 3 4. 1 x − 3 y − 9. 1 x + y = 1
Đặt 1 x − 3 y = a ; 1 x + y = b ta được hệ phương trình 2 3 a + 6 b = 3 4 a − 9 b = 1
Đáp án: D
Nghiệm (x; y) của hệ phương trình 2 x + 2 y + 1 2 x + y = 3 4 x + 2 y + 3 2 x + y = 1 là:
A. 13 60 ; − 7 30
B. − 13 60 ; − 7 30
C. − 13 60 ; 7 30
D. 13 60 ; 7 30
ĐK: x + 2 y ≠ 0 y + 2 x ≠ 0 ⇔ x ≠ − 2 y y ≠ − 2 x
Đặt 1 x + 2 y = u ; 1 2 x + y = v (u, v ≠ 0)
Khi đó, ta có hệ phương trình:
⇔ 2 u + v = 3 4 u + 3 v = 1 ⇔ v = 3 − 2 u 4 u + 3 3 − 2 u = 1 ⇔ v = 3 − 2 u u = 4 t m ⇔ u = 4 v = − 5 t m ⇒ 1 x + 2 y = 4 1 2 x + y = − 5 ⇔ 4 x + 8 y = 1 − 10 x − 5 y = 1 ⇔ x = − 13 60 t m y = 7 30 t m
Đáp án:C
Cho hệ phương trình y = 2 x + 20 y = 2 m - 4 x + 10 . Tìm m để hệ phương trình đã cho vô nghiệm
A. m = 3
B. m = 1
C. m = -2
D. m = -1
Đáp án A
Nghiệm phương trình y = 2x + 20 được biểu diễn bởi đường thẳng ( d 1 ): y =2x +20.
Nghiệm phương trình y = (2m - 4)x + 10 được biểu diễn bởi đường thẳng ( d 2 ): y = (2m – 4)x + 10.
Để hệ phương trình đã cho vô nghiệm khi 2 đường thẳng d 1 // d 2
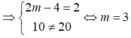
giải các bất phương trình sau
a, x^3+5x^2+7x-12>0
b, x^5+x^4-15x^3-5x^2+34x<-24
Không giải hệ phương trình, dự đoán số nghiệm của hệ − x + 5 y = − 1 5 x + y = 2
A. Vô số nghiệm
B. Vô nghiệm
C. Có nghiệm duy nhất
D. Có hai nghiệm phân biệt
Xét hệ phương trình − x + 5 y = − 1 5 x + y = 2 có − 1 5 ≠ 5 1 nên hệ phương trình có nghiệm duy nhất
Đáp án: C
Cho (x; y; z) là nghiệm của hệ phương trình 36 x 2 y − 60 x 2 + 25 y = 0 36 y 2 z − 60 y 2 + 25 z = 0 36 z 2 x − 60 z 2 + 25 x = 0 . Giá trị nhỏ nhất của A = x + y + z là:
A. A = 0
B. A = 5 2
C. A = 1
D. A = −2
36 x 2 y − 60 x 2 + 25 y = 0 36 y 2 z − 60 y 2 + 25 z = 0 36 z 2 x − 60 z 2 + 25 x = 0 ⇔ y = 60 x 2 36 x 2 + 25 z = 60 y 2 36 y 2 + 25 x = 60 z 2 36 z 2 + 25 ⇒ x , y , z ≥ 0
Nhận thấy x = y = z = 0 là một nghiệm của hệ phương trình
Xét x > 0; y > 0; z > 0 áp dụng bất đẳng thức Cosi cho hai số không âm ta có:
36 x 2 + 25 ≥ 2 36 x 2 .25 = 60 | x | ≥ 60 x ⇒ y ≤ x
Chứng minh tương tự, ta được z ≤ y ; x ≤ z ⇒ x ≤ z ≤ y ≤ x ⇒ x = y = z
Thay vào phương trình (1) ta được 36 x 3 – 60 x 2 + 25 x = 0 ⇔ x = 5 6
hay x = y = z = 5 6
Suy ra giá trị nhỏ nhất của A = x + y + z = 0 (khi x = y = z = 0)
Đáp án:A