Giai phương trình sau
\(x^3-12=13x\)
Giải các phương trình sau:
a) x + 5 = − x + 3 ; b) 1 2 2 x + 3 + 1 3 x = 1 12 ;
c) 10 x + 1 2 − 11 = 0 ; d) 2 x + 1 5 1 3 x − 5 4 = 0 .
Giai phương trình theo phương trình trùng phương :
a : x^4 - 13x^2 + 36 =0
b : 5x^4 + 3x^2 - 8 =0
c : 2x^4 + 3x^2 +2 =0
a) \(x^4-13x^2+36=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-2\\x=-3\end{matrix}\right.\)
b) \(5x^4+3x^2-8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(5x^2+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)( do \(5x^2+8\ge8>0\))
c: Ta có: \(2x^4+3x^2+2=0\)
Đặt \(a=x^2\)
Phương trình tương đương là: \(2a^2+3a+2=0\)
\(\text{Δ}=3^2-4\cdot2\cdot2=9-16=-7\)
Vì Δ<0 nên phương trình vô nghiệm
Vậy: Phương trình \(2x^4+3x^2+2=0\) vô nghiệm
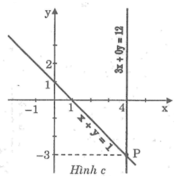
Minh họa hình học tập nghiệm của mỗi hệ phương trình sau: x + y = 1 3 x + 0 y = 12
*Ta có: x + y = 1 ⇔ y = -x + 1
Cho x = 0 thì y = 1 ⇒ (0; 1)
Cho y = 0 thì x = 1 ⇒ (1; 0)
*Ta có: 3x + 0y = 12 ⇔ x = 4
Hai đường thẳng cắt nhau tại P(4; -3) nên nghiệm của hệ phương trình là (x; y) = (4; -3)
Đồ thị:
Giải các phương trình sau: 13 2 x + 1 - 13 x - 12 = 0

Vậy nghiệm của phương trình đã cho là x = 0
Giải các phương trình sau: 5 - 2 x 3 + x + 1 x - 1 3 x - 1 = x + 2 1 - 3 x 9 x - 3
5 - 2 x 3 + x + 1 x - 1 3 x - 1 = x + 2 1 - 3 x 9 x - 3 Đ K X Đ : x ≠ 1 3 ⇔ 5 - 2 x 3 x - 1 3 3 x - 1 + 3 x + 1 x - 1 3 3 x - 1 = x + 2 1 - 3 x 3 3 x - 1
⇔ (5 – 2x)(3x – 1) + 3(x + 1)(x – 1) = (x + 2)(1 – 3x)
⇔ 15x – 5 – 6 x 2 + 2x + 3 x 2 – 3 = x – 3 x 2 + 2 – 6x
⇔ - 6 x 2 + 3 x 2 + 3 x 2 + 15x + 2x – x + 6x = 2 + 5 + 3
⇔ 22x = 10 ⇔ x = 5/11 (thỏa mãn)
Vậy phương trình có nghiệm x = 5/11
Giai các bất phương trình sau:
a) 5x-2\(\ge\)8
b) 4+3x\(\ge\)2x+1
c) 2(x-5)<8
d) \(\frac{13x-12}{12}>\frac{9x+1}{3}-\frac{8x+1}{4}\)
g) \(\frac{1}{2}x-2>2+\frac{5}{6}x\)
h) 3c-5<3d-5
Giải phương trình sau :
x^6+x^5-13x^4-14x^3+x+1
Giải các phương trình sau: x - 1 3 x = 2
Giải các bất phương trình sau bằng 1 3 x ≥ x + 1
Vẽ đồ thị của hàm số 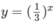 và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
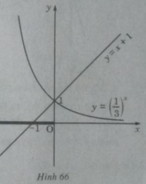
Khi x < 0 đồ thị của hàm số 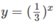 nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;0]
nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;0]