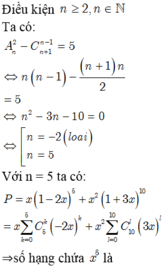cho P(x)= (1+x)(1+2x)(1+3x)......(1+10x)
Tìm hệ số của x^2 trong khai triển trên
MQ
Những câu hỏi liên quan
15. Số hạng chính giữa trong khai triển (3x + 2y)^4 là?
18. Tìm hệ số của x^7 trong khai triển : h(x)= x(2 + 3x)^9 là?
19. Tìm hệ số của x^7 trong khai triển g(x)= (1+x)^7 + (1-x)^8 + (2+x)^9 là?
15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
Đúng 1
Bình luận (3)
1) tìm hệ số của x^5 trong khai triển x(2x−1)6+(3x−1)8
2) tìm hệ số của x3 trong khai triển x(1+2x)n với n t/mAnx=12
tìm hệ só của x trong khai triển của (1+x)(1-2x)(1+3x)(1-4x)...(1-2018x)
Hệ số của x trong khai triển đã cho là: \(1-2+3-4+...+2017-2018=\left(-1\right)+\left(-1\right)+...+\left(-1\right)=-1009\).
Đúng 1
Bình luận (0)
Tìm hệ số của
x
5
trong khai triển đa thức của
x
(
1
-
2
x
)
5
+
x
2
(
1
+
3
x
)
10
A. 61204 B. 3160 C. 3320 D. 61268
Đọc tiếp
Tìm hệ số của x 5 trong khai triển đa thức của x ( 1 - 2 x ) 5 + x 2 ( 1 + 3 x ) 10
A. 61204
B. 3160
C. 3320
D. 61268
Hệ số của x5 trong khai triển x(1-2x)5 là (-2)4.C54
Hệ số của x5 trong khai triển x2(1+3x)10 là 33.C103
Do đó hệ số của x5 trong khai triển x(1-2x)5+ x2(1+3x)10 là
(-2)4.C54 + 33.C103= 3320
Chọn C
Đúng 0
Bình luận (0)
1: hệ số của số hang chứa x8 trong khai triển \(\left(\frac{1}{x^4}+\sqrt[2]{x^5}\right)^{12}\)
2: hệ số của số hang chứa x16 trong khai triển \(\left[1-x^2\left(1-x^2\right)\right]^{16}\)
3: hệ số của số hạng chứa x5 trong khai triển \(x\left(1-2x\right)^5+x^2\left(1+3x\right)^{10}\)
\(\left(x^{-4}+x^{\frac{5}{2}}\right)^{12}\) có SHTQ: \(C_{12}^kx^{-4k}.x^{\frac{5}{2}\left(12-k\right)}=C^k_{12}x^{30-\frac{13}{2}k}\)
Số hạng chứa \(x^8\Rightarrow30-\frac{13}{2}k=8\Rightarrow\) ko có k nguyên thỏa mãn
Vậy trong khai triển trên ko có số hạng chứa \(x^8\)
b/ \(\left(1-x^2+x^4\right)^{16}\)
\(\left\{{}\begin{matrix}k_0+k_2+k_4=16\\2k_2+4k_4=16\end{matrix}\right.\)
\(\Rightarrow\left(k_0;k_2;k_4\right)=\left(8;8;0\right);\left(9;6;1\right);\left(10;4;2\right);\left(11;2;3\right);\left(12;0;4\right)\)
Hệ số của số hạng chứa \(x^{16}\):
\(\frac{16!}{8!.8!}+\frac{16!}{9!.6!}+\frac{16!}{10!.4!.2!}+\frac{16!}{11!.2!.3!}+\frac{16!}{12!.4!}=...\)
c/ SHTQ của khai triển \(\left(1-2x\right)^5\) là \(C_5^k\left(-2\right)^kx^k\)
Số hạng chứa \(x^4\) có hệ số: \(C_5^4.\left(-2\right)^4\)
SHTQ của khai triển \(\left(1+3x\right)^{10}\) là: \(C_{10}^k3^kx^k\)
Số hạng chứa \(x^3\) có hệ số \(C_{10}^33^3\)
\(\Rightarrow\) Hệ số của số hạng chứa \(x^5\) là: \(C_5^4\left(-2\right)^4+C_{10}^3.3^3\)
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x
2
-
2
x
n
C
n
0...
Đọc tiếp
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x 2 - 2 x n = C n 0 x 2 n + C n 1 x 2 n - 1 - 2 x + . . . + C n n - 1 x 2 - 2 x n - 1 + C n n - 2 x n n ∈ ℕ *
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. 11520
B. 11250
C. 12150
D. 10125
1. Tìm hệ số của số hạng x^4 trong khai triển left(x-3right)^92. Tìm hệ số của số hạng chứa x^{12}y^{13} trong khai triển left(2x+3yright)^{25}3. Tìm hệ số của số hạng chứa x^4 trong khai triển left(dfrac{x}{3}-dfrac{3}{x}right)^{12}4. Tìm hệ số của số hạng không chứa x trong khai triển left(x^2-dfrac{1}{x}right)^65. Tìm hệ số của số hạng không chứa x trong khai triển left(x+dfrac{1}{x^4}right)^{10}
Đọc tiếp
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
Hệ số của
x
5
trong khai triển biểu thức P(x) x
(
2
x
-
1
)
6
+
(
3
x
-
1
)
8
bằng A. -13848 B. 13368 C. 13848 D. -13368
Đọc tiếp
Hệ số của x 5 trong khai triển biểu thức P(x) = x ( 2 x - 1 ) 6 + ( 3 x - 1 ) 8 bằng
A. -13848
B. 13368
C. 13848
D. -13368
Chọn D
Số hạng tổng quát của khai triển ![]()
![]()
![]()
Số hạng chứa
x
5
trong A(x) là![]()
Số hạng tổng quát của khai triển ![]()
![]()
![]()
Số hạng chứa
x
5
trong B(x) là ![]()
Vậy hệ số của số hạng chứa x 5 trong khai triển P(x) đã cho là 240-13608 = -13368.
Đúng 0
Bình luận (0)
Tìm hệ số của
x
5
trong khai triển biểu thức
P
x
(
1
-
2
x
)
n
+
x
2
(
1
+
3
x
)
2...
Đọc tiếp
Tìm hệ số của x 5 trong khai triển biểu thức P = x ( 1 - 2 x ) n + x 2 ( 1 + 3 x ) 2 n . Biết rằng A n 2 - C n + 1 n - 1 = 5
A. 3240
B. 3320
C. 3210
D. 3340