Lực F nhận giá trị âm khi nào
HT
Những câu hỏi liên quan
Câu 17: Thể tích của một miếng sắt là 2dm3. Lực đẩy tác dụng lên miếng sắt khi nhúng chìm trong nước sẽ nhận giá trị nào trong các giá trị sau: A. F 15N B. F 20N C. F 25N D. F 10N
Đọc tiếp
Câu 17: Thể tích của một miếng sắt là 2dm3. Lực đẩy tác dụng lên miếng sắt khi nhúng chìm trong nước sẽ nhận giá trị nào trong các giá trị sau:
A. F = 15N B. F = 20N C. F = 25N D. F = 10N
Đổi: \(2dm^3=2.10^{-3}m^3\)
Lực đẩy Acsimet tác dụng vào miếng sắt khi nhúng chìm trong nước là:
\(F_A=d.V=10000.2.10^{-3}=20N\)
=> B\(\text{F = 20N }\)
Đúng 3
Bình luận (1)
Tam thức bậc hai f(x) = x 2 - 12x - 13 nhận giá trị không âm khi và chỉ khi:
A. x ∈ (-1;13)
B. x ∈ R\[-1;13]
C. x ∈ [-1;13]
D. x ∈ (- ∞ ;-1] ∪ [13;+ ∞ )
Chọn D.
Tam thức bậc hai f(x) = x 2 - 12x - 13 nhận giá trị không âm khi và chỉ khi
f(x) ≥ 0 ⇔
x
2
- 12x - 13 ≥ 0 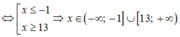
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
1
/
(
x
-
2
)
có đồ thị như ở Hình 52Quan sát đồ thị và cho biết:- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào. - Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
Đọc tiếp
Cho hàm số f ( x ) = 1 / ( x - 2 ) có đồ thị như ở Hình 52
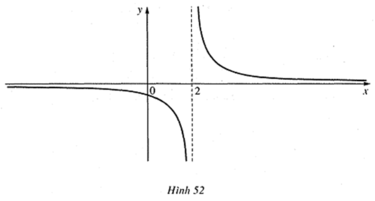
Quan sát đồ thị và cho biết:
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị 0.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị 0.
Đúng 0
Bình luận (0)
cho ham so f(x)=x^2-1. Tìm tất cả giá trị của x sao cho f(1-x) nhận giá trị âm
Cho hàm số f(x) = x2 -1 . Tìm các giá trị của x sao cho f(1-x) nhận giá trị âm
Cho hàm số
y
f
(
x
)
-
1
2
x
nhận giá trị âm thì: A. x 0 B. x 0 C. x 0 D. chưa biết dấu của x
Đọc tiếp
Cho hàm số y = f ( x ) = - 1 2 x nhận giá trị âm thì:
A. x > 0
B. x < 0
C. x = 0
D. chưa biết dấu của x
Để hàm số 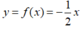 nhận giá trị âm thì x phải dương
nhận giá trị âm thì x phải dương
Chọn đáp án A
Đúng 0
Bình luận (0)
Thể tích của một miếng sắt là 2 d m 3 . Lực đẩy tác dụng lên miếng sắt khi nhúng chìm trong nước sẽ nhận giá trị nào trong các giá trị sau:
A. F = 15N
B. F = 20N
C. F = 25N
D. F = 10N
Ta có: 2 d m 3 = 0,002 m 3
Lực đẩy Ác-si-mét tác dụng lên miếng sắt khi miếng sắt được nhúng chìm trong nước là: F n ư ớ c = d n ư ớ c . V s ắ t = 10000 . 0 , 002 = 20 N
⇒ Đáp án B
Đúng 0
Bình luận (0)
f (x) = x² - 2(m-1)x + 4m. Tìm m để f(x) luôn nhận giá trị âm
\(f\left(x\right)=x^2-2\left(m-1\right)x+4m.\)
Để \(f\left(x\right)< 0\forall x\in R.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a< 0.\\\Delta'< 0.\end{matrix}\right.\)
Mà \(a=1>0.\)
\(\Rightarrow f\left(x\right)< 0\Leftrightarrow x\in\phi.\)
Đúng 0
Bình luận (2)
Mk trl sai câu này r nhg ko xoá đc bn thông cảm nhé.
Đúng 0
Bình luận (0)
f (x) = mx² - 2(m-1)x + 4m. Tìm m để f(x) luôn nhận giá trị âm
\(f\left(x\right)< 0\forall x\in R.\\ \Leftrightarrow\left\{{}\begin{matrix}m< 0.\\\Delta'=m^2-2m+1-4m^2< 0.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0.\\\Delta'=-3m^2-2m+1< 0.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0.\\\left[{}\begin{matrix}m< -1.\\m>\dfrac{1}{3}.\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow m< -1.\\ \Leftrightarrow m\in\left(-\infty;-1\right).\)
Đúng 0
Bình luận (0)



