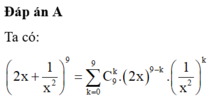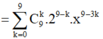TK
Những câu hỏi liên quan
1. Tìm hệ số của số hạng x^4 trong khai triển left(x-3right)^92. Tìm hệ số của số hạng chứa x^{12}y^{13} trong khai triển left(2x+3yright)^{25}3. Tìm hệ số của số hạng chứa x^4 trong khai triển left(dfrac{x}{3}-dfrac{3}{x}right)^{12}4. Tìm hệ số của số hạng không chứa x trong khai triển left(x^2-dfrac{1}{x}right)^65. Tìm hệ số của số hạng không chứa x trong khai triển left(x+dfrac{1}{x^4}right)^{10}
Đọc tiếp
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
Trong khai triển \(\left(2x^3-\dfrac{3}{x^2}\right)^{10}\). Hãy tìm hệ số của \(x^{10}\)
\(\left(2x^3-\dfrac{3}{x^2}\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.2^k.3^{10-k}.x^{3k}.\dfrac{1}{x^{2\left(10-k\right)}}\)
\(x^{10}=\dfrac{x^{3k}}{x^{20-2k}}\Leftrightarrow3k-20+2k=10\Leftrightarrow5k=30\Leftrightarrow k=6\)
\(\Rightarrow he-so:2^k.3^{10-k}=2^6.3^4=..\)
Đúng 1
Bình luận (0)
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x
2
-
2
x
n
C
n
0...
Đọc tiếp
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x 2 - 2 x n = C n 0 x 2 n + C n 1 x 2 n - 1 - 2 x + . . . + C n n - 1 x 2 - 2 x n - 1 + C n n - 2 x n n ∈ ℕ *
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. 11520
B. 11250
C. 12150
D. 10125
Tìm hệ số của \(x^{12}\) trong khai triển \(\left(2x-x^2\right)^{10}\)
\(\left(2x-x^2\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}\cdot\left(2x\right)^{10-k}\cdot\left(-x^2\right)^k=\sum\limits^{10}_{k=0}C^k_{10}\cdot2^{10-2k}\cdot\left(-1\right)^k\cdot x^{10+k}\)
\(x^{12}\Rightarrow\)\(10+k=12\Rightarrow k=2\)
Hệ số của số hạng đó: \(C^2_{10}\cdot2^6\cdot\left(-1\right)^2=2880\)
Đúng 0
Bình luận (0)
Tìm hệ số của số hạng chứa
x
3
trong khai triển của
2
x
+
1
x
2
9
với x
≠
0 A. 4608 B. 128 C. 164 D. 36
Đọc tiếp
Tìm hệ số của số hạng chứa x 3 trong khai triển của 2 x + 1 x 2 9 với x ≠ 0
A. 4608
B. 128
C. 164
D. 36
Tìm hệ số của số hạng chứa
x
3
trong khai triển của
2
x
+
1
x
2
9
với
x
≠
0
A. 4608 B. 128 C. 164 D. 36
Đọc tiếp
Tìm hệ số của số hạng chứa x 3 trong khai triển của 2 x + 1 x 2 9 với x ≠ 0
A. 4608
B. 128
C. 164
D. 36
tìm hệ số của số hạng chứa x6 trong khai triển (3+2x)^8
\(\left(3+2x\right)^8=\sum\limits^8_{k=0}C^k_8.3^{8-k}.2^k.x^k\)
\(\Rightarrow\) Hệ số của số hạng chứa \(x^6\) là \(C^6_8.3^{8-6}.2^6=16128\)
Đúng 0
Bình luận (0)
Gọi a là hệ số không chứa x trong khai triển khai triển nhị thức Niu-tơn
x
2
−
2
x
n
C
n
0
x
2
n
+
C
n...
Đọc tiếp
Gọi a là hệ số không chứa x trong khai triển khai triển nhị thức Niu-tơn x 2 − 2 x n = C n 0 x 2 n + C n 1 x 2 n − 1 − 2 x + … + C n n − 1 x 2 − 2 x n − 1 + C n n − 2 x n (n là số nguyên dương).
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. a = 11520
B. a = 11250
C. a = 12150
D. a = 10125
Đáp án A
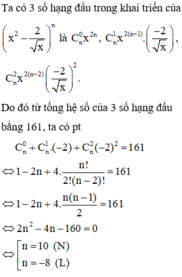
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
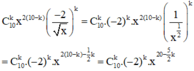
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho
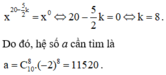
Đúng 0
Bình luận (0)
Tìm hệ số của x^5 trong khai triển: (2x-1)^4+(2x-1)^5+(2x-1)^6+(2x-1)^7
Xét khai triển: \(\left(2x-1\right)^n\) với \(n\ge5\)
SHTQ: \(C_n^k.\left(2x\right)^k.\left(-1\right)^{n-k}=C_n^k.2^k.\left(-1\right)^{n-k}.x^k\)
Số hạng chứa \(x^5\Rightarrow k=5\) có hệ số \(C_n^5.2^5.\left(-1\right)^{n-5}\)
Do đó hệ số của \(x^5\) trong khai triển đã cho là:
\(C_5^5.2^5.\left(-1\right)^0+C_6^5.2^5.\left(-1\right)^1+C_7^5.2^5.\left(-1\right)^2=...\)
Đúng 1
Bình luận (0)