Chứng minh EFGH là hình thoi
Đọc tiếp
Chứng minh EFGH là hình thoi
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
CI
Những câu hỏi liên quan
Cho hình thoi ABCD tâm O. Trên tia đối của các tia BA, CB, DC, AD lần lượt các điểm E, F, G, H sao cho BE = CF = DG = AH.
a) Chứng minh tứ giác EFGH là hình bình hành.
b) Chứng minh điểm O là tâm đối xứng của hình bình hành EFGH.
c) Hình thoi ABCD phải có điều kiện gì để EFGH trở thành hình thoi ?
a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
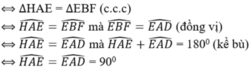
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.
Đúng 0
Bình luận (0)
H24
SGK Toán 8 tập 1– Chân trời sáng tạo
21 tháng 7 2023 lúc 22:37
Quan sát hình 21. Chứng minh rằng tứ giác \(EFGH\) là hình thoi.
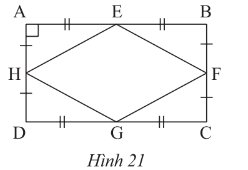
Xét \(\Delta HAE\) và \(\Delta FBE\) ta có:
\(AH = BF\) (gt)
\(\widehat {{\rm{HAE}}} = \widehat {{\rm{FBE}}} = 90^\circ \) (gt)
\(AE = BE\) (gt)
Suy ra \(\Delta HAE = \Delta FBE\) (c-g-c)
Suy ra \(HE = EF\)
Chứng minh tương tự ta có: \(EF = GF\); \(GF = GH\); \(GH = HE\)
Suy ra \(HE = EF = FG = GH\)
Suy ra \(EFGH\) là hình thoi
Đúng 0
Bình luận (0)
Cho hình thoi ABCD tâm O. Trên tia đối của các tia BA, CB, DC, AD lần lượt các điểm E, F, G, H sao cho BE = CF = DG = AH.
a) Chứng minh tứ giác EFGH là hình bình hành.
b) Chứng minh điểm O là tâm đối xứng của hình bình hành EFGH.
c) Hình thoi ABCD phải có điều kiện gì để EFGH trở thành hình thoi ?
giúp với
a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có tâm là O.Trên tia đối của các tia BA,CB,DC,DA lần lượt lấy các điểm E,F,G,H sao cho BE=CF=DG=AH
a)Chứng minh EFGH là hình bình hành
b)Chứng minh O là tâm đối xứng của hình bình hành
c)Hình thoi ABCD cần có thêm điều kiện gì để EfGH là hình thoi
a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
Đúng 0
Bình luận (0)
Bài 1. Cho tứ giác ABCD có E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Biết AC = BD và AC vuông góc BD. Chứng minh: a) EFGH là hình bình hành. b) EFGH là hình chữ nhật. c) EFGH là hình thoi. d) EFGH là hình vuông
Cho hình thoi ABCD tâm O. Trên tia đối của các tia BA, CB,DC,AD lần lượt là các điểm E, F, G, H sao cho BE=CF=DG=AH.
a) Chứng minh tứ giác ÈGH là hình bình hành
b) Chứng minh điểm 0 là tâm đối xứng của hình bình hành EFGH
c)Hình thoi ABCD phải có điều kiện gì để EFGH trở thành hình thoi ?
Cho ABCD là hình chữ nhật. Gọi E,G,H,F lần lượt là trung điểm của AB,BC,CD,DA. Chứng minh
a) EFGH là hình thoi
b) EFGH là hình bình hành
Bài 1
Áp dụng tính chất đường trung bình vào
*\large\Delta ABD có: AE=EB, BH=HD EH //AD, EH=\frac{AD}{2}
*\large\Delta ACD có: AF=CF, DG=GC GF //AD, GF=\frac{AD}{2}
*\large\Delta ABC có: AE=EB, BF=CF EF //AD, EF=\frac{BC}{2}
*\large\Delta BCD có: BH=HD, DG=GC HG //AD, GH=\frac{BC}{2}
Tứ giác EFGH có: EH//GF//AD, EH=GF=\frac{AD}{2}
EFGH là hbh
a)Để EFGH là hcn EH \perp \ EF, EF \perp \ FG, FG \perp \ GH
mà EH//AD, EF//BC, FG//AD , GH//BC
AB \perp \ BC
\widehat{ADC}+\widehat{BCD}=90^o
__________________
mình lớp 5 mong bạn thông cảm
Đúng 0
Bình luận (0)
Cho tứ giác EFGH. Gọi M, N, P, Q lần lượt là trung điểm các cạnh EF, FG, GH, HE.
a) Chứng minh MNPQ là hình bình hành
b) Nếu EFGH là hình thoi thì MNPQ là hình gì? Vì sao?
c) Nếu EFGH là hình chữ nhật thì MNPQ là hình gì? Vì sao?
Cho hình thoi ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.
Chứng minh EFGH là hình bình hành
Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình
=>EH//BD và EH=BD/2
Xét ΔBCD có
G,F lần lượt là trung điểm của CD,CB
=>GF là đường trung bình
=>GF//BD và GF=BD/2
=>EH//GF và EH=GF
=>EFGH là hình bình hành
Đúng 0
Bình luận (1)