cho điểm A nằm ngoài đường tròn (O;R), từ A kẻ 2 tiếp tuyến AB,AC với B và C là 2 tiếp điểm. Kẻ cát tuyến ADE đến (O). Gọi H là trung điểm của DE.
a/ Chứng minh 5 điểm A,B,H,O,C cùng thuộc một đường tròn
b/ Chứng minh HA là tia phân giác của góc BHC
c/ DE cắt BC tại I. Gọi K là giao điểm của OA và BC. Chứng minh: tứ giác OKIH nội tiếp từ đó suy ra AB^2 = AI.AH
d/ Cho AB = R căn 3; OH = R/2. Tính IH theo R
H24
Những câu hỏi liên quan
Cho đường tròn (O) và điểm A nằm bên ngoài (O). Kẻ 2 tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm). Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB AC, d không đi qua tâm O). Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau ở K. Chứng minh K thuộc một đường thẳng cố định khi d thay đổi và thỏa mãn điều kiện đề bài.HELP MEEEEEEEEEE
Đọc tiếp
Cho đường tròn (O) và điểm A nằm bên ngoài (O). Kẻ 2 tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm). Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB< AC, d không đi qua tâm O). Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau ở K. Chứng minh K thuộc một đường thẳng cố định khi d thay đổi và thỏa mãn điều kiện đề bài.
HELP MEEEEEEEEEE
ΔKBO=ΔKCO
=>KB=KC
=>KO là trung trực của BC
ΔKCO đồng dạng với ΔCIO
=>OC/OI=OK/OC
=>OC^2=OI*OK
=>OI*OK=ON^2
=>OI/ON=ON/OK
=>ΔOIN đồng dạng với ΔONK
=>gócc ONI=góc OKN
Tương tự, ta có: OI/OM=OM/OK
=>ΔMKO đồng dạng với ΔIMO
=>góc MKO=góc IMO=góc INO
=>góc MKD=góc NKD
=>K,M,N thẳng hàng
=>K luôn thuộc MN
Đúng 0
Bình luận (0)
Bài 6: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BCa) Chứng minh OA vuông góc với BC tại Hb) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.ADAH.AOc) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của đường tròn tâm...
Đọc tiếp
Bài 6: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC
a) Chứng minh OA vuông góc với BC tại H
b) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.AD=AH.AO
c) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của đường tròn tâm (O)
d) Gọi I là trung điểm cạnh AB, qua I vẽ đừng thẳng vuông góc với cạnh AO tại M và đường thẳng này cắt đường thẳng DF tại N. Chứng minh: ND=NA
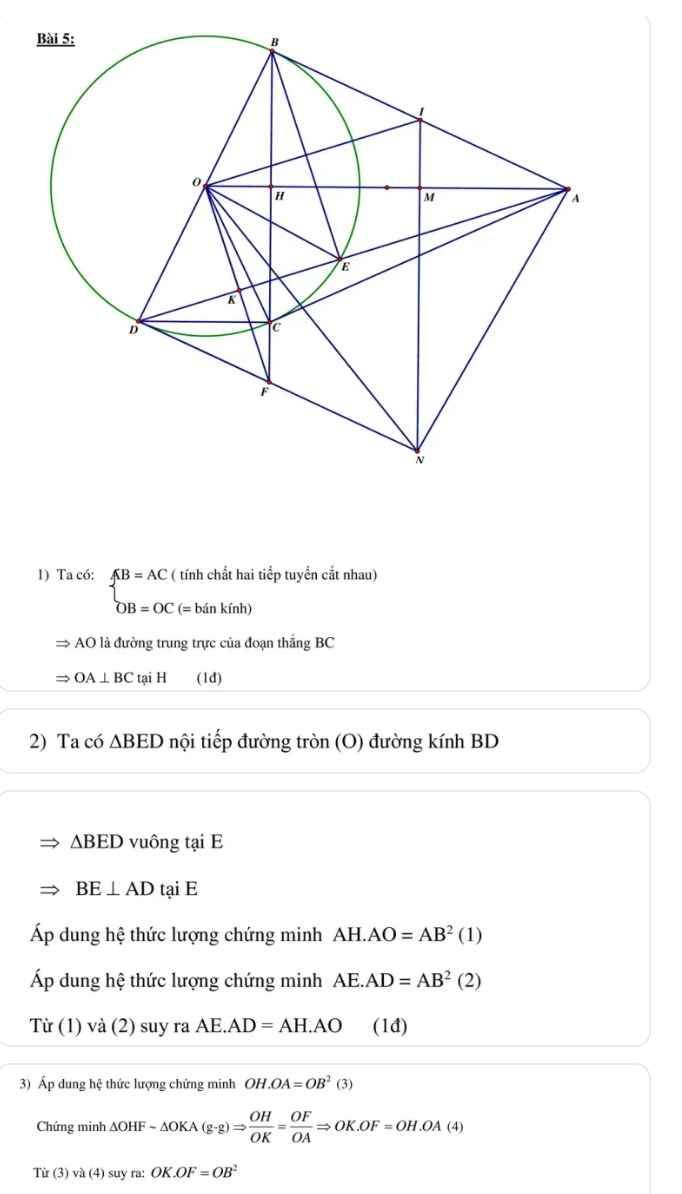

Bạn tham khảo cách làm này của mình nhé
Đúng 1
Bình luận (2)
Cần gấpCho đường trong (O) và điểm A nằm ngoài đường tròn. Vẽ các tiếp tuyến AM và AN với đường tròn (O) (M,N là tiếp điểm). Qua A vẽ 1 đường thẳng cắt đường tròn (O) tại 2 điểm B và C (B nằm giữa A và C). Gọi H là trung điểm của BC.a) Chứng minh tứ giác ANHM nội tiếp đường tròn tâm (O)b) Chứng minh: AN^2AB.ACc) Đường thẳng qua B song song với AN cắt MN tại E. Chứng minh: EH//NC
Đọc tiếp
Cần gấp
Cho đường trong (O) và điểm A nằm ngoài đường tròn. Vẽ các tiếp tuyến AM và AN với đường tròn (O) (M,N là tiếp điểm). Qua A vẽ 1 đường thẳng cắt đường tròn (O) tại 2 điểm B và C (B nằm giữa A và C). Gọi H là trung điểm của BC.
a) Chứng minh tứ giác ANHM nội tiếp đường tròn tâm (O)
b) Chứng minh: AN^2=AB.AC
c) Đường thẳng qua B song song với AN cắt MN tại E. Chứng minh: EH//NC
Cho đoạn thẳng AB 4cm gọi Ô là trung điểm của AB vẽ đường tròn tâm Ô bán kính 1cm cắt OA tại M OB tại N a) xác định trên đoạn thẳng AB một điểm là tâm của một đường tròn bán kính 2cm đi qua O sao cho điểm N nằm trong đường tròn đó còn điểm N nằm ngoài đường tròn đóc) đường tròn ở phần b cắt đường tròn tâm O bán kính 1cm tại C và D hãy so sánh tổng BC+CO với BM
Đọc tiếp
Cho đoạn thẳng AB =4cm gọi Ô là trung điểm của AB vẽ đường tròn tâm Ô bán kính 1cm cắt OA tại M OB tại N
a) xác định trên đoạn thẳng AB một điểm là tâm của một đường tròn bán kính 2cm đi qua O sao cho điểm N nằm trong đường tròn đó còn điểm N nằm ngoài đường tròn đó
c) đường tròn ở phần b cắt đường tròn tâm O bán kính 1cm tại C và D hãy so sánh tổng BC+CO với BM
Cho đường tròn (O, Đ) điểm A nằm ngoài đường tròn OA = 2R vẽ tiếp tuyến AB; AC (B, C là tiếp điểm)
a) Chứng minh AB ACb) Chứng minh tâm giâc ABC đềuc) Đường thẳng OA cắt đường tròn (O) tại M, N. Chứng minh ABNC là hình thoiCho 2 đường tròn đồng tâm, tâm O bán kính R và tâm O bán kính R' (R>R'). Điểm M nằm ngoài 2 đường tròn. Vẽ MA là tiếp tuyến của đường tròn tâm O bán kính R. MB là tiếp tuyến của đường tròn tâm O bán kính R'. Chứng minh rằng đường trung trực của đoạn thẳng AB đi qua trung điểm của OM
Cho đường tròn (o) và điểm B nằm bên ngoài đường tròn. Từ B vẽ tiếp tuyến BA,BC đến đường tròn(A,C là tiếp điểm), và vẽ cát tuyến BDEsao cho D nằm giữa B và E (D,E thuộc (O)). Gọi F là trung điểm của ED.a) Chứng minh: điểm A,B,C,F,O cùng thuôc một đường trònb) Gọi H là giao điểm của OB và AC. Chứng minh: BH.BOBD.BEGọi I là giao điểm của AC và DE. Chứng minh tứ giác OHDE nội tiếp và ID.EBEI.DBd) Gọi K là giao điểm của đoạn thẳng OB với...
Đọc tiếp
Cho đường tròn (o) và điểm B nằm bên ngoài đường tròn. Từ B vẽ tiếp tuyến BA,BC đến đường tròn(A,C là tiếp điểm), và vẽ cát tuyến BDE
sao cho D nằm giữa B và E (D,E thuộc (O)). Gọi F là trung điểm của ED.
a) Chứng minh: điểm A,B,C,F,O cùng thuôc một đường tròn
b) Gọi H là giao điểm của OB và AC. Chứng minh: BH.BO=BD.BE
Gọi I là giao điểm của AC và DE. Chứng minh tứ giác OHDE nội tiếp và ID.EB=EI.DB
d) Gọi K là giao điểm của đoạn thẳng OB với đường tròn. Chứng minh: EK là tia phân giác của DE^H
Cho A là một điểm nằm ngoài đường tròn left(O;Rright). Qua A vẽ hai tiếp tuyến AB, AC (B, C là tiếp điểm). H là giao điểm của AO và BC. Kẻ đường kính BD; AD cắt left(Oright) tại E.a. Chứng minh: OA perp BC và CD // OA.b. Chứng minh: AH.AO AE.AD và ∠AHE ∠ADO.c. Cho OB 2cm, OA 4 cm. Chứng minh: △ABC là tam giác đều và tính diện tích △ABC
Đọc tiếp
Cho A là một điểm nằm ngoài đường tròn \(\left(O;R\right)\). Qua A vẽ hai tiếp tuyến AB, AC \((\)B, C là tiếp điểm\()\). H là giao điểm của AO và BC. Kẻ đường kính BD; AD cắt \(\left(O\right)\) tại E.
a. Chứng minh: OA \(\perp\) BC và CD // OA.
b. Chứng minh: AH.AO \(=\) AE.AD và ∠AHE \(=\) ∠ADO.
c. Cho OB = 2cm, OA = 4 cm. Chứng minh: △ABC là tam giác đều và tính diện tích △ABC
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD tại C
Ta có: BC\(\perp\)CD
OA\(\perp\)BC
Do đó: OA//CD
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔDBA vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(3\right)\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(4\right)\)
Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)
=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{EAH}\) chung
Do đó: ΔAEH đồng dạng với ΔAOD
=>\(\widehat{AHE}=\widehat{ADO}\)
c: Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AO là phân giác của góc BAC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=60^0\)
Xét ΔOBA vuông tại B có \(BO^2+BA^2=OA^2\)
=>\(BA^2+2^2=4^2\)
=>\(BA^2=12\)
=>\(BA=2\sqrt{3}\left(cm\right)\)
Xét ΔBAC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔBAC đều
=>\(S_{ABC}=\left(2\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=12\cdot\dfrac{\sqrt{3}}{4}=3\sqrt{3}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho đường tròn tâm O, đường kính AB. M là một điểm nằm trên đoạn thẳng OB (M khác O và khác B). Đường thẳng d qua M và vuông góc với AB cắt đường tròn (O) tại C, D. Trên tia MD lấy điểm E nằm ngoài đường tròn (O). Đường thẳng AE cắt (O) tại điểm thứ hai I khác A, đường thẳng BE cắt (O) tại điểm thứ hai K khác B. Gọi H là giao điểm của BI và d.a. Chứng minh tứ giác MBEI nội tiếp được trong một đường tròn. Xác định tâm của đường tròn này.b...
Đọc tiếp
Cho đường tròn tâm O, đường kính AB. M là một điểm nằm trên đoạn thẳng OB (M khác O và khác B). Đường thẳng d qua M và vuông góc với AB cắt đường tròn (O) tại C, D. Trên tia MD lấy điểm E nằm ngoài đường tròn (O). Đường thẳng AE cắt (O) tại điểm thứ hai I khác A, đường thẳng BE cắt (O) tại điểm thứ hai K khác B. Gọi H là giao điểm của BI và d.
a. Chứng minh tứ giác MBEI nội tiếp được trong một đường tròn. Xác định tâm của đường tròn này.
b. Chứng minh các tam giác IEH và MEA đồng dạng với nhau.
c. Chứng minh EC.ED = EH.EM
d Chứng minh khi E thay đổi, đường thẳng HK luôn đi qua một điểm cố định
a/ Ta có
^AIB=90 (góc nt chắn nửa đường tròn) => BI vuông góc AE
d vuông góc với AB tại M
=> M và I cùng nhìn BE dưới 1 góc 90 => M; I cùng nằm trên đường tròn đường kính BE => MBEI là tứ giác nội tiếp
b/ Xét tam giác vuông MEA và tam giác vuông IEH có ^AEM chung => tg MEA đồng dạng với tg IEH
d/ Xét tg ABE có
BI vuông góc AE
ME vuông góc AB
=> H là trực tâm cuat tg ABE
Ta có ^AKB =90 (góc nt chắn nửa đường tròn => AK vuông góc với BE
=> AK đi qua H (trong tam giác 3 đường cao đồng quy
=> Khi E thay đổi HK luôn đi qua A cố định
Đúng 0
Bình luận (0)
Cô hướng dẫn nhé :)
a. Ta thấy góc MBE = góc BIE = 90 độ nên từ giác MBEI nội tiếp đường tròn đường kính BE, vậy tâm là trung điểm BE.
b. \(\Delta IEH\sim\Delta MEA\left(g-g\right)\) vì có góc EIH = góc EMA = 90 độ và góc E chung.
c. Từ câu b ta có : \(\frac{IE}{EM}=\frac{EH}{EA}\Rightarrow EH.EM=IE.EA\) Vậy ta cần chứng minh \(EC.ED=IE.EA\)
Điều này suy ra được từ việc chứng minh \(\Delta IED\sim\Delta CEA\left(g-g\right)\)
Hai tam giác trên có góc E chung. góc DIE = góc ACE (Tứ giác AIDC nội tiếp nên góc ngoài bằng góc tại đỉnh đối diện)
d. Xét tam giác ABE, ta thấy do I thuộc đường trong nên góc AIB = 90 độ. Vậy EM và BI là các đường cao, hay H là trực tâm của tam giác ABE. Ta thấy AK vuông góc BE, AH vuông góc BE, từ đó suy ra A, H ,K thẳng hàng. Vậy khi E thay đổi HK luôn đi qua A.
Tự mình trình bày để hiểu hơn nhé . Chúc em học tốt ^^
Đúng 0
Bình luận (0)
Cho đường tròn (O;R) và điểm A nằm ngoài (O;R). Đường tròn đường kính AO cắt đường tròn (O;R) tại M và N. Đường thẳng d qua A cắt (O;R) tại B và C ( d không đi qua O; B nằm giữa A và C). Gọi H là trung điểm BC.1) CM: AM là tiếp tuyến của (O;R) và H thuộc đường tròn đường kính AO.2) Đường thẳng qua B vuông góc với OM cắt MN ở D. CMR:a) góc AMN góc BDNb) DH song song MCc) HB + HD CD
Đọc tiếp
Cho đường tròn (O;R) và điểm A nằm ngoài (O;R). Đường tròn đường kính AO cắt đường tròn (O;R) tại M và N. Đường thẳng d qua A cắt (O;R) tại B và C ( d không đi qua O; B nằm giữa A và C). Gọi H là trung điểm BC.
1) CM: AM là tiếp tuyến của (O;R) và H thuộc đường tròn đường kính AO.
2) Đường thẳng qua B vuông góc với OM cắt MN ở D. CMR:
a) góc AMN = góc BDN
b) DH song song MC
c) HB + HD > CD



