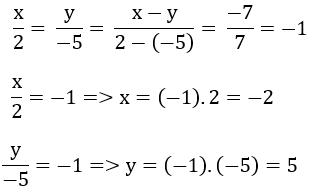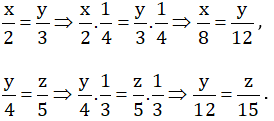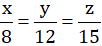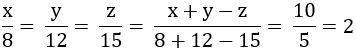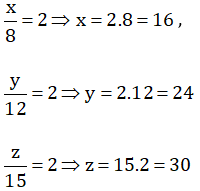HD
Những câu hỏi liên quan
Tìm x,y thuộc Z
a) 2x+3y= -1 và 3x-1 phần y = -7 phần 2
b) x+3 phần 2y-1 = 5 phần 3 và 4x+5y=18
c) x phần y = 63 phần 96 và UWCLN (a,b)=17
d) x phần y = 5 phần 7 và BCNN ( a,b) = 105
Tìm số chung
a) 1 phần 5 < x phần 30 < 1 phần 4
b) 5 phần 8 < 4 phần x < 5 phần 7
giúp mình với minh tk cho
Tìm x,y
a) x+y phần 2=x-y phần 3=y+1 phần 4
b) x phần 2=y phần 5 biết xy=20
giúp mình với!!!
Tìm x,y thuộc Z biết 3 x phần 5 y 3 5 và x y 6b,x 4 y 3 4 3 và x-y=5
giúp mik với mik đang cần gấp lắm nha
x-2 phần y-1= 4 phần 3 với x-y=2
Tìm x và y
giúp mình giải bài này với nha
Cảm ơn
\(\frac{x-2}{y-1}=\frac{4}{3}\Rightarrow\frac{x-2}{4}=\frac{y-1}{3}\)
Theo t/c dãy tỉ số = nhau:
\(\frac{x-2}{4}=\frac{y-1}{3}=\frac{x-2-y+1}{4-3}=\frac{x-y-1}{1}=2-1=1\)
=> x - 2 = 4 => x = 4 + 2 = 6
=> y - 1 = 3 => y = 3 + 1 = 4
Đúng 0
Bình luận (0)
GIẢI GIÚP MỀNH VỚI
Tìm x,y,z:
a)|1-x|+|y-2/3|+|x+z|=0
b)|1/4-x|+|x+y+z|+|2/3+y|=0
c)|15/32-x|+4/25-y|+|z-14/31|=0
X phần 6 = y phần 3 biết x×y =3 tìm x,y
Giải gấp giúp mình với ạ
Đặt x/6 = y/3 = k
=> x=6k và y = 3k
Ta có : xy = 3
=> 18k^2 = 3
=> k^2 = 1/6
=> k = ±√1/6 = ±√6 / 6
Vậy (x;y) = (√6;√6 /2);(-√6;-√6 /2)
Đúng 0
Bình luận (0)
Bài 1:cho ba số 6;8;24a)Tìm số x sao cho x cùng với 3 số trên tạo thành 1 tỉ lệ thứcb)Có thể lập được bao nhiêu tỉ lệ thứcBài 2:cho tỉ lệ thức 3x-y phần x+y3 phần 4.tính x phần yBài 3:Tìm x;y;za)xy phần 5z phần 2 và 3x-5y+2z-54b)x-1 phần 2-2 phần 3z-3 phần 4 và x-2y+3z14Bài 4:Tìm x;y;za)x^3 phần 8y^3 phần 64z^3 phần 216 va x^2+y^3+z^3b)x/y/z3/4/5 và x^n2+y^2-3z^2-236Bài 5:Tìm t1,t2,...,t9 biết t1-1 phần 9t2-2 phần 8.....t9-9 phần 1 và t1+t2+.....+t9180Bài 6:Số học sinh lớp 7A,7B,7C tỉ l...
Đọc tiếp
Bài 1:cho ba số 6;8;24
a)Tìm số x sao cho x cùng với 3 số trên tạo thành 1 tỉ lệ thức
b)Có thể lập được bao nhiêu tỉ lệ thức
Bài 2:cho tỉ lệ thức 3x-y phần x+y=3 phần 4.tính x phần y
Bài 3:Tìm x;y;z
a)x=y phần 5=z phần 2 và 3x-5y+2z=-54
b)x-1 phần 2=-2 phần 3=z-3 phần 4 và x-2y+3z=14
Bài 4:Tìm x;y;z
a)x^3 phần 8=y^3 phần 64=z^3 phần 216 va x^2+y^3+z^3
b)x/y/z=3/4/5 và x^n2+y^2-3z^2=-236
Bài 5:Tìm t1,t2,...,t9 biết t1-1 phần 9=t2-2 phần 8=.....=t9-9 phần 1 và t1+t2+.....+t9=180
Bài 6:Số học sinh lớp 7A,7B,7C tỉ lệ với 10,9,8.Số học sinh lớp 7A nhiều hơn số học sinh lớp 7B là 5 em. hỏi mỗi lớp có bao nhiêu học sinh
Bài 7:có 3 tủ sách đựng tất cả 2250 cuốn. nếu chuyển 100 cuốn từ tủ 1 sang tử 3 thì số sách ở tủ 1,2,3 tỉ lệ với 16,15,14.hỏi trước khi chuyển mỗi tủ có bao nhiêu cuốn sách
Làm nhanh giúp mình nhé. Thứ 3 phải nộp rồi
tìm x y thuộc Z :
x - 3 phần y - 2 = 3 phần 2 và x + y = 1
ai giúp mình với . cho 3 like
a) tìm hai số x và y biết x:2 = y: (-5) và x-y =-7
b) tìm ba số x,y,z biết x phần 2 = y phần 3 ,y phần 4 và z phần 5 và x+y-z=10
cảm ơn trước ak
a) Ta có: \(x:2=y:\left(-5\right)\)
nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)
mà x-y=-7
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(-2;5)
b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)
nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)
Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x+y-z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(16;24;30)
Đúng 2
Bình luận (0)
b)
Do đó ta có
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Đúng 0
Bình luận (0)