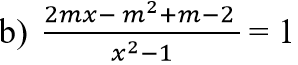Điều kiện của phương trình là x ≠ -3. Khi đó ta có

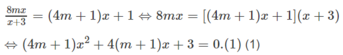
 Với m = -1/4 phương trình (1) trở thành

    3x + 3 = 0 ⇔ x = -1

    Với m ≠ -1/4 phương trình (1) là một phương trình bậc hai có

    Δ' = (2m - 1)2 ≥ 0

    Lúc đó phương trình (1) có hai nghiệm

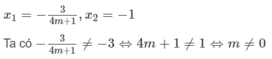
 Kết luận

    Với m = 0 hoặc m = -1/4 phương trình đã cho có một nghiệm x = -1.

    Với m ≠ 0 và m ≠ -1/4 phương trình đã cho có hai nghiệm

    x = -1 và 

Điều kiện của phương trình là x ≠ 2. Khi đó ta có

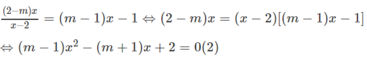
Với m = 1 phương trình (2) có dạng

    -2x + 2 = 0 ⇔ x = 1

    Với m ≠ 1 thì phương trình (2) là một phương trình bậc hai có :

     Δ = (m - 3)2 ≥ 0

    Lúc đó phương trình (2) có hai nghiệm

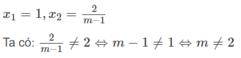
Kết luận :

    Với m = 1 và m = 2 phương trình đã cho có một nghiệm là x = 1.

    Với m ≠ 1 và m ≠ 2 phương trình đã cho có hai nghiệm

    x = 1 và 

Từ PT (1) ta có: y = (a + 1)x – (a + 1) (*)

Thế vào PT (2) ta được:

x + (a – 1) [(a + 1)x – (a + 1)] = 2 ⇔ x + ( a 2 – 1 ) x – ( a 2 – 1 ) = 2 x + (a² – 1)x – (a² – 1) = 2

⇔ a 2 x = a 2 + 1   ( 3 )

Với a ≠ 0 , phương trình (3) có nghiệm duy nhất x = a 2 + 1 a 2 . Thay vào (*) ta có:

y = a + 1 a 2 + 1 a 2 − a + 1 = a + 1 a 2 + 1 − a 2 a + 1 a 2 = a 3 + a + a 2 + 1 − a 3 − a 2 a 2 = a + 1 a 2

Suy ra hệ phương trình đã cho có nghiệm duy nhất ( x ;   y ) = a 2 + 1 a 2 ; a + 1 a 2  

⇒ x + y = a 2 + 1 a 2 + a + 1 a 2 = a 2 + a + 2 a 2

Đáp án: A

a) Với m= 2, ta có phương trình:  x 2 + 2 x − 3 = 0

Ta có:  a + b + c = 1 + 2 − 3 = 0                                                             

Theo định lý Viet, phương trình có 2 nghiệm: 

x 1 = 1 ;   x 2 = − 3 ⇒ S = 1 ;   − 3 .                                                                             

b) Chứng minh rằng phương trình luôn có nghiệm  ∀ m .

Ta có:  Δ ' = m − 1 2 − 1 + 2 m = m 2 ≥ 0 ;    ∀ m                                           

Vậy phương trình luôn có nghiệm  ∀ m .                                              

c) Theo định lý Viet, ta có: x 1 + x 2 = − 2 m + 2 x 1 . x 2 = 1 − 2 m                                                             

Ta có:

x 1 2 . x 2 + x 1 . x 2 2 = 2 x 1 . x 2 + 3 ⇔ x 1 . x 2 x 1 + x 2 − 2 = 6 ⇒ 1 − 2 m − 2 m + 2 − 2 = 6 ⇔ 2 m 2 − m − 3 = 0                  

Ta có: a − b + c = 2 + 1 − 3 = 0 ⇒ m 1 = − 1 ;   m 2 = 3 2                                                  

Vậy m= -1 hoặc m= 3/2 

Cô làm câu b thôi nhé :)

Ta có hệ \(\hept{\begin{cases}mx+4y=10-m\\x+my=4\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(4-my\right)+4y=10-m\\x=4-my\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}\left(4-m^2\right)y=10-5m\left(1\right)\\x=4-my\end{cases}}\)

Với \(4-m^2=0\Leftrightarrow m=2\) hoặc \(m=-2\)

Xét m =2, phương trình (1) tương đương 0.x = 0. Vậy hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)

Xét m = -2, phương trình (1) tương đương 0.x = 20. Vậy hệ phương trình vô nghiệm.

Với \(4-m^2\ne0\Leftrightarrow m\ne2\) và \(m\ne-2\), phương trình (1) tương đương \(y=\frac{10-5m}{4-m^2}=\frac{5}{2+m}\)

Từ đó : \(x=\frac{8-m}{2+m}\)

Kết luận: 

+ m = 2, hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)

+ m = - 2, hệ phương trình vô nghiệm.

+ \(m\ne2;m\ne-2\) hệ có 1 nghiệm duy nhất \(\hept{\begin{cases}x=\frac{8-m}{2+m}\\y=\frac{5}{2+m}\end{cases}}\)

Chúc em học tập tốt :)

hehe
Hỏi từ lâu nhưng bây giờ em trả lời lại cho vui

a) Ta có : |2ax + 3| = 5(1) ⇔ |2ax + 3| = |5| ⇔ 2ax + 3 = 5

hoặc 2ax + 3 = -5 ⇔ 2ax = 2 hoặc 2ax = -8 ⇔ ax = 1 hoặc ax = -4

Nếu a = 0 ⇒ (1) vô nghiệm

Nếu a ≠ 0 ⇒ (1) có hai nghiệm phân biệt : x = 1/a , x = -4/a

b)Điều kiện xác định của phương trình là ∀ x; x ≠ 1 và x ≠ - 1.

Khi đó : (2mx- m2 + m - 2 )/(x2 - 1) = 1 (2)

(2)⇔ 2mx – m2 + m – 2 = x2 – 1 ⇔ x2 – 2mx + m2 – m + 1 = 0 (3)

Ta có : Δ’ = m2 – m2 + m -1 = m – 1

Nếu m – 1 < 0 ⇔ m < 1 ⇒ (3) vô nghiệm ⇒ (2) vô nghiệm

Nếu m – 1 = 0 ⇔ m = 1 ⇒ (3) có nghiệm kép x1 = x2 = 1 ⇒ (2) vô nghiệm

Nếu m - 1 > 0 có m > l =0 (3) có hai nghiệm phân biệt

x1 = m – √(m -1) ; x2 = m + √(m -1) (hiển nhiên x2 > x1)

Vì m > 1 nên x2 > 1 ⇒ x2 luôn là nghiệm của (2). Còn x1 ≤ 1.

Nên : Nếu x1 = -1 ⇔ m – √(m – 1) = - 1 ⇔ m + 1 = √( m – 1)

⇔ m2 + 2m +1 = m – 1(vì m + 1 > 0)

⇔ m2 + m + 2 = 0 phương trình này vô nghiệm tức là x1 ≠ -1 với mọi m > 1.

Vậy x1 = 1 ⇔ m = 2

Tóm lại : m ≤ 1 thì (2) vô nghiệm

m > 1 và m ≠ 2 thì (2) có hai nghiệm phân biệt :

x1 = m – √(m -1) ; x2 = m + √(m -1)

m = 2 thì (2) có một nghiệm x = 3.