PD
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A và góc
ABC
^
30
0
. Xác định góc giữa hai vectơ
CA
→
;
CB
→
. A.
60
0
B. ...
Đọc tiếp
Cho tam giác ABC vuông tại A và góc ABC ^ = 30 0 . Xác định góc giữa hai vectơ CA → ; CB → .
A. 60 0
B. 120 0 .
C. - 30 0 .
D. 30 0 .
cho tam giác ABC cân tại A, có AB=6cm, BAC=120. Gọi M là trung điểm BC.chứng minh vectơ AB +vecto MC= vecto AC+ vecto MB / vecto AB- vecto CM/
Xem chi tiết
cho tam giác ABC cân tại A, có AB=6cm, BAC=120. Gọi M là trung điểm BC.chứng minh vectơ AB +vecto MC= vecto AC+ vecto MB / vecto AB- vecto CM/
Xem chi tiết
Sửa đề: Chứng minh \(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
\(\overrightarrow{AB}-\overrightarrow{MB}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AM}\)
\(\overrightarrow{AC}-\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{CM}=\overrightarrow{AC}\)
Do đó: \(\overrightarrow{AB}-\overrightarrow{MB}=\overrightarrow{AC}-\overrightarrow{MC}\)
=>\(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
Đúng 0
Bình luận (0)
cho hình lăng trụ đứng ABCA'B'C' có đáy là tam giác cân tại A, AB=a, góc BAC=120°. góc giữa (A'BC) và (ABC)=60°. tính VABCA'B'C'
Câu 4 : Cho tam giác ABC vuông cân tại A và AB =√2 . Tính vectơ CA . vectơ BC . Câu 5 : Cho ABC có trọng tâm G . Biểu diễn vectơ AG theo hai vectơ AB , AC được kết quả là? Câu 6 : Cho các vectơ a,b thỏa mãn|vectơ a | =1 , |vectơ B | =2 , | vectơ a - vectơ b| =3 . Tích vectơ a. vectơ b bằng? Câu 7 : Cho hình vuông ABCD có cạnh bằng a . Tính| vectơ AB - vectơ AD + vectơ CD | .
Câu 4:
Áp dụng định lý Pytago
\(BC^2=AB^2+AC^2\Rightarrow BC=2\)
Ta có:
\(\overrightarrow{CA}.\overrightarrow{BC}=-\overrightarrow{CA}.\overrightarrow{CB}=-\dfrac{CA^2+CB^2-AB^2}{2}=-\dfrac{2+4-2}{2}=-2\)
Câu 5:
Gọi M là trung điểm BC
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Mà: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 6:
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=3\)
\(a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=9\)
\(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1^2+2^2-9}{2}=-2\)
Câu 7:
\(\left|\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{CD}\right|=\left|\overrightarrow{DB}+\overrightarrow{CD}\right|\)
\(=\left|\overrightarrow{DB}-\overrightarrow{DC}\right|=\left|\overrightarrow{CB}\right|=BC=a\)
Đúng 3
Bình luận (0)
cho khối chóp sabcd có đáy là tam giác cân tại a có ab=ac=4a, góc BAC=120. Gọi M là trung điểm cảu BC, N là trung điểm của AB, SAM là tam giác cân tại S và thuộc mặt phẳng vuông góc với đáy. SA=a . căn 2. Góc giữa SN và (ABC) là
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, widehat{BAC}120^o, ABACa. Tam giác SAB vuông tại B, tam giác SAC vuông tại C, góc giữa hai mặt phẳng left(SABright) và left(ABCright) bằng 60^o. Gọi H là hình chiếu vuông góc của điểm S lên mặt phẳng left(ABCright). Chứng minh rằng HB vuông góc AB và tính thể tích khối chóp S.ABC theo a
Đọc tiếp
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(\widehat{BAC}=120^o\), \(AB=AC=a\). Tam giác \(SAB\) vuông tại \(B\), tam giác \(SAC\) vuông tại \(C\), góc giữa hai mặt phẳng \(\left(SAB\right)\) và \(\left(ABC\right)\) bằng \(60^o\). Gọi \(H\) là hình chiếu vuông góc của điểm \(S\) lên mặt phẳng \(\left(ABC\right)\). Chứng minh rằng \(HB\) vuông góc \(AB\) và tính thể tích khối chóp \(S.ABC\) theo \(a\)
Cho hình lăng trụ đứng
A
B
C
.
A
B
C
có tam giác ABC cân tại A và
A
B
a
,
B
A
C
^
120
°
. Góc giữa đường thẳng AB′ và mặt phẳng (ABC) bằng
60
°
. Diện tích xung quanh của khối lăng trụ
A
B
C...
Đọc tiếp
Cho hình lăng trụ đứng A B C . A ' B ' C ' có tam giác ABC cân tại A và A B = a , B A C ^ = 120 ° . Góc giữa đường thẳng AB′ và mặt phẳng (ABC) bằng 60 ° . Diện tích xung quanh của khối lăng trụ A B C . A ' B ' C ' là
A. 3 a 2
B. 3 + 2 3 a 2
C. 2 3 a 2
D. 3 a 2
Đáp án B
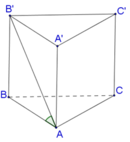

Vậy diện tích xung quanh của lăng trụ đứng ABCA′B′C′ là
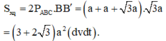
Đúng 0
Bình luận (0)
cho hình chóp sabc có sa vuông góc với abc và sa = ab hãy tính góc giữa cặp vectơ bs và vectơ ab
A. 120°
B.135°
C.60°
D.45°
Giúp mìk vs




