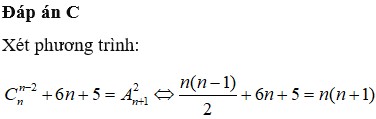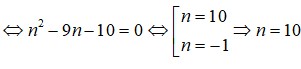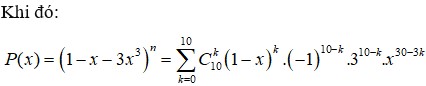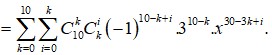NT
Những câu hỏi liên quan
1) tìm hệ số của x^5 trong khai triển x(2x−1)6+(3x−1)8
2) tìm hệ số của x3 trong khai triển x(1+2x)n với n t/mAnx=12
C35 Cho n là số nguyên dương lẻ , thõa mãn 5 C ¹N - C² N =15 . Tìm hệ số của x² trong khai triển nhị thức Niuton ( 2x+ 1/x²)^n A. 60 B. 90 C. 80 D .110 C14: số Nghiệm của pt √3x+5=2 là A. 3 B. 0 C. 2 D. 1 Giúp cho e
Với n là số nguyên dương thỏa mãn \(3A^{n-2}_n+C^3_n=40\). Hệ số của x6 trong khai triển \(\left(2x-\dfrac{1}{x}\right)^{2n}\) là:
A.-1024 B.1024 C.-1042 D.1042
Tìm hệ số chứa x^10 trong khai triển f(x)=(1/4x^2+x+1)(x+2)^3n với n là số tự nhiên thỏa mãn hệ thức A^3n+C^n-2n=14n
Xem chi tiết
 Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
Đúng 0
Bình luận (0)
Gọi a là hệ số không chứa x trong khai triển khai triển nhị thức Niu-tơn
x
2
−
2
x
n
C
n
0
x
2
n
+
C
n...
Đọc tiếp
Gọi a là hệ số không chứa x trong khai triển khai triển nhị thức Niu-tơn x 2 − 2 x n = C n 0 x 2 n + C n 1 x 2 n − 1 − 2 x + … + C n n − 1 x 2 − 2 x n − 1 + C n n − 2 x n (n là số nguyên dương).
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. a = 11520
B. a = 11250
C. a = 12150
D. a = 10125
Đáp án A
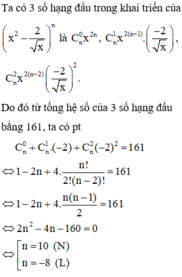
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
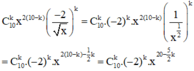
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho
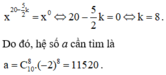
Đúng 0
Bình luận (0)
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x
2
-
2
x
n
C
n
0...
Đọc tiếp
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
Gọi x là hệ số không chứa x trong khai triển nhị thức Niu – tơn
x 2 - 2 x n = C n 0 x 2 n + C n 1 x 2 n - 1 - 2 x + . . . + C n n - 1 x 2 - 2 x n - 1 + C n n - 2 x n n ∈ ℕ *
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. 11520
B. 11250
C. 12150
D. 10125
Bài 2 a) Tìm hệ số của x^3 trong khai triển của (x+2/x^2)^6
b) Tìm hệ số của x^7 trong khai triển (3-2x)^15
c) Tìm số hạng không chứa x trong khai triển (2x-1/x^2)^6
(^: là mũ nhé mn,bài này mình vừa học ở trường nhưng chưa hiểu mn giúp chi tiết,cảm ơn mn ^•^)
\(\left(x+2.x^{-2}\right)^6=\sum\limits^6_{k=0}C_6^kx^k.2^{6-k}.\left(x^{-2}\right)^{6-k}=\sum\limits^6_{k=0}C_6^k2^{6-k}x^{3k-12}\)
Số hạng chứa \(x^3\Rightarrow3k-12=3\Rightarrow k=5\)
\(\Rightarrow\) Hệ số: \(C_6^5.2^1=12\)
\(\left(3-2x\right)^{15}=\sum\limits^{15}_{k=0}C_{15}^k3^k.\left(-2\right)^{15-k}.x^{15-k}\)
Số hạng chứa \(x^7\Rightarrow15-k=7\Rightarrow k=8\)
\(\Rightarrow\) Hệ số: \(C_{15}^8.3^8.\left(-2\right)^7\)
\(\left(2x-x^{-2}\right)^6=\sum\limits^6_{k=0}C_6^k2^k.x^k.\left(-1\right)^{6-k}.\left(x^{-2}\right)^{6-k}=\sum\limits^6_{k=0}C_6^k2^k\left(-1\right)^{6-k}.x^{3k-12}\)
Số hạng ko chứa x \(\Rightarrow3k-12=0\Rightarrow k=4\)
Hệ số: \(C_6^42^4\left(-1\right)^2=240\)
Tìm hệ số của
x
4
trong khai triển
P
(
x
)
(
1
-
x
-
3
x
3
)
n
với n là số tự nhiên thỏa mãn hệ thức
C
n
n
-
2...
Đọc tiếp
Tìm hệ số của x 4 trong khai triển P ( x ) = ( 1 - x - 3 x 3 ) n với n là số tự nhiên thỏa mãn hệ thức C n n - 2 + 6 n + 5 = A n + 1 2
A. 210
B. 840
C. 480
D. 270
Biết tổng các hệ số của ba số hạng đầu trong khai triển \(\left(x^3+\dfrac{1}{x^2}\right)^n\) bằng 11. Tìm hệ số của \(x^7\) trong khai triển đó.
\(C_n^0+C_n^1+C_n^2=11\)
\(\Rightarrow1+n+\dfrac{n\left(n-1\right)}{2}=11\)
\(\Leftrightarrow n^2+n-20=0\Rightarrow\left[{}\begin{matrix}n=4\\n=-5\left(loại\right)\end{matrix}\right.\)
\(\left(x^3+\dfrac{1}{x^2}\right)^4\) có SHTQ: \(C_4^k.x^{3k}.x^{-2\left(4-k\right)}=C_4^k.x^{5k-8}\)
\(5k-8=7\Rightarrow k=3\)
Hệ số: \(C_4^3=4\)
Đúng 0
Bình luận (0)