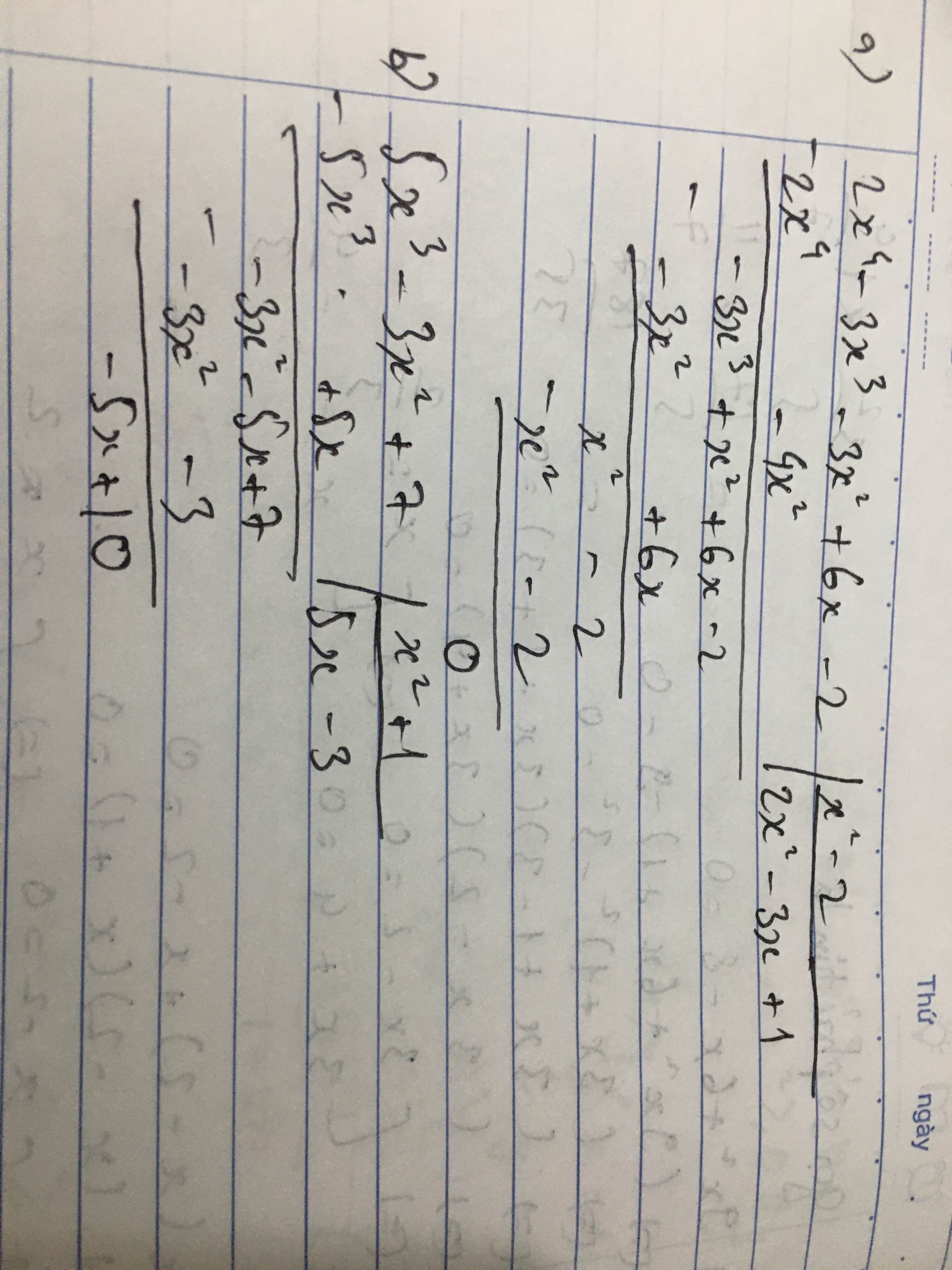Thực hiện phép tính: (2x4 - 3x3 - 3x2 -2 + 6x) : (x2 - 2)
DT
Những câu hỏi liên quan
Sắp xếp đa thức theo lũy thừa giảm dần của biến rồi làm phép chia: (2x4 – 3x3 – 3x2 – 2 + 6x) : (x2 – 2)
2x4 – 3x3 – 3x2 – 2 + 6x = 2x4 – 3x3 – 3x2 + 6x – 2
Thực hiện phép chia:
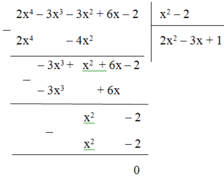
Vậy (2x4 – 3x3 – 3x2 + 6x – 2) : (x2 – 2) = 2x2 – 3x + 1.
Đúng 1
Bình luận (0)
( 2x4 -3x3 -3x2 +6x -2 ) : ( x2 -2 )
\(=\dfrac{2x^4-4x^2-3x^3+6x+x^2-2}{x^2-2}=2x^2-3x+1\)
Đúng 1
Bình luận (0)
Chia đa thức cho đa thức:
a) (2x4-3x3-3x2-2+6x) : (x2-2)
b) (5x3-3x2+7) : (x2+1)
a) \(\left(2x^4-3x^3-3x^2-2+6x\right):\left(x^2-2\right)=2\left(x^2-\dfrac{3}{2}x+\dfrac{1}{2}\right)\left(x^2-2\right):\left(x^2-2\right)=2x^2-3x+1\)
Đúng 0
Bình luận (0)
a: \(\dfrac{2x^4-3x^3-3x^2+6x-2}{x^2-2}\)
\(=\dfrac{2x^4-4x^2-3x^3+6x+x^2-2}{x^2-2}\)
\(=2x^2-3x+1\)
b: \(\dfrac{5x^3-3x^2+7}{x^2+1}\)
\(=\dfrac{5x^3+5x-3x^2-3-5x+10}{x^2+1}\)
\(=5x-3+\dfrac{-5x+10}{x^2+1}\)
Đúng 0
Bình luận (0)
Vận dụng giải bài toán tròn tính huống mở đầu
Tìm đa thức P sao cho A = B. P, trong đó A = 2x4 – 3x3 – 3x2 + 6x – 2 và B = x2 – 2
Thực hiện phép tính
(2x4+x3+3x2+4x+9):(x2+1)
lấy 2x4 chia x2 ra kết quả rồi lại nhân ngược với x2+1 lấy cái 2x4+x3+3x2+4x+9 trừ đi cái vừa tính
Đúng 0
Bình luận (0)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)
a) Thực hiện phép chia đa thức (2x4 - 6x3 +12x2 - 14x + 3) cho đa thức (x2 – 4x +1)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)
Đúng 3
Bình luận (0)
Thực hiện phép tính:
x2(x+8y)
(2x4 + 6x3 + 6x):2x
a: \(=x^3+8x^2y\)
b: \(=x^3+3x^2+3\)
Đúng 0
Bình luận (0)
Bài 1 .Với giá trị nào của x thì đa thức d- trong mỗi phép chia sau có giá trị bằng 0?
a. (2x4 - 3x3 + 4x2 + 1) : (x2 - 1 ) b. (x5 + 2x4 + 3x2 + x -3 ) : (x2 + 1)Giải hộ va aka: \(\dfrac{2x^4-3x^3+4x^2+1}{x^2-1}=\dfrac{2x^4-2x^2-3x^3+3x+6x^2-6-3x+7}{x^2-1}\)
\(=2x^2-3x+6+\dfrac{-3x+7}{x^2-1}\)
Để dư bằng 0 thì -3x+7=0
=>x=7/3
b: \(\dfrac{x^5+2x^4+3x^2+x-3}{x^2+1}\)
\(=\dfrac{x^5+x^3+2x^4+2x^2-x^3-x+x^2+1+2x-4}{x^2+1}\)
\(=x^3+2x^2-x+1+\dfrac{2x-4}{x^2+1}\)
Để đư bằng 0 thì 2x-4=0
=>x=2
Đúng 0
Bình luận (0)