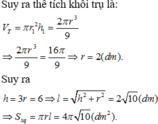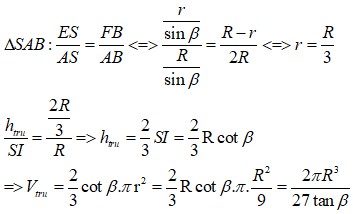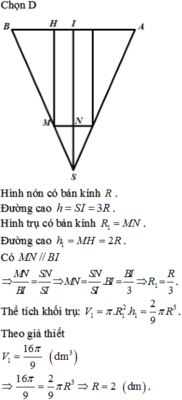Một hình trụ có đường cao bằng đường kính đáy. Biết rằng thể tích hình trụ là 128 π c m 3 . Tính diện tích xung quanh của nó.
PB
Những câu hỏi liên quan
Câu 1: Thể tích hình trụ là 375 π , chiều cao 15. Tính diện tích xung quanh hình trụ.
Câu 2: Một hình trụ có diện tích toàn phần bằng diện tích hình tròn có bán kính 12cm, chiều cao hình trụ bằng 2 lần bán kính đáy. Tính bán kính đáy hình trụ đó.
1:
V=pi*r^2*h
=>r^2*15*pi=375pi
=>r^2=25
=>r=5
Sxq=2*pi*r*h=2*5*15*pi=150pi
Đúng 0
Bình luận (0)
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó, Người ta thả vào đó một khối trụ và đo được thể tích nước tràn ra ngoài là
16
π
3
d
m
3
. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón, các điểm trên đường tròn đáy còn lại đều thuộc các đường sinh c...
Đọc tiếp
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó, Người ta thả vào đó một khối trụ và đo được thể tích nước tràn ra ngoài là 16 π 3 d m 3 . Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón, các điểm trên đường tròn đáy còn lại đều thuộc các đường sinh của hình nón (như hình vẽ) và khối trụ có chiều cao bằng đường kính đáy của hình nón. Tính diện tích xung quanh S x q của bình nước
A. 9 π 10 2 d m 2
B. 4 π 10 d m 2
C. 4 π d m 2
D. 2 π d m 2
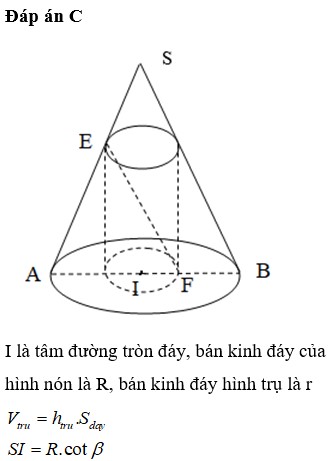
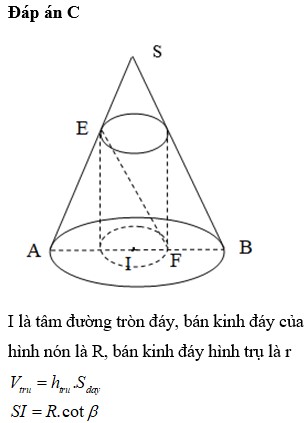
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là
β
. Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng. A.
2
R
3
π
9
tan
β...
Đọc tiếp
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là β . Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng.
A. 2 R 3 π 9 tan β
B. 4 R 3 π 27 tan β
C. 2 R 3 π 27 tan β
D. 2 R 3 π 3 tan β
Đáp án C
I là tâm đường tròn đáy, bán kinh đáy của hình nón là R, bán kinh đáy hình trụ là r
V t r u = h t r u . S d a y
S I = R . c o t β
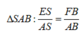
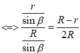
⇔ r = R 3
h t r u S I = 2 R 3 R ⇒ h t r u = 2 3 S I = 2 3 R . c o t β
⇒ V t r u = 2 3 c o t β . π . r 2 = 2 πR 3 27 tanβ
Đúng 0
Bình luận (0)
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là
β
. Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng A.
2
R
3
π
9
tan
β
B.
4
R...
Đọc tiếp
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là β . Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng
A. 2 R 3 π 9 tan β
B. 4 R 3 π 27 tan β
C. 2 R 3 π 27 tan β
D. 2 R 3 π 3 tan β
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là
β
. Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng A.
2
R
3
π
9
tan
...
Đọc tiếp
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là β . Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng
A. 2 R 3 π 9 tan β
B. 4 R 3 π 27 tan β
C. 2 R 3 π 27 tan β
D. 2 R 3 π 3 tan β
Một bình đựng nước dạng hình nón (không đáy) đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó. Người ta thả vào đó một khối trụ và đo dược thể tích nước tràn ra ngoài là
16
π
9
d
m
3
. Biết rằng một mặt của khối trụ nằm trên mặt trên của hình nón, các điểm trên đường tròn đáy còn lại đều thuộc các đường sinh của hình nón (như hình vẽ) và khối trụ...
Đọc tiếp
Một bình đựng nước dạng hình nón (không đáy) đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó. Người ta thả vào đó một khối trụ và đo dược thể tích nước tràn ra ngoài là
16
π
9
d
m
3
. Biết rằng một mặt của khối trụ nằm trên mặt trên của hình nón, các điểm trên đường tròn đáy còn lại đều thuộc các đường sinh của hình nón (như hình vẽ) và khối trụ có chiều cao bằng đường kính đáy của hình nón. Diện tích xung quanh
S
x
q
của bình nước là: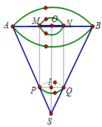
![]()
![]()
![]()
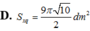
Một bình đựng nước dạng hình nón (không có nắp đáy), đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài là
16
π
9
d
m
3
. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao...
Đọc tiếp
Một bình đựng nước dạng hình nón (không có nắp đáy), đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài là 16 π 9 d m 3 . Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của hình nón (như hình vẽ dưới). Tính bán kính đáy của bình nước.
![]()
![]()
![]()
![]()
Một hình trụ có bán kính đường tròn đáy là 6cm ,chiều cao 9cm. Hãy tính: Thể tích của hình trụ
(Lấy π = 3,142 làm tròn kết quả đến hàng đơn vị )
Thể tích hình trụ là :
V = π R 2 .h = 3,142.62.9 ≈ 1018 ( c m 3 )
Đúng 0
Bình luận (0)
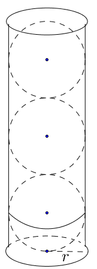
Người ta bỏ vào một chiếc hộp hình trụ ba quả bóng tennis hình cầu bằng nhau, biết rằng đáy hình trụ bằng hình tròn lớn trên quả bóng, chiều cao của hình trụ gấp 3 lần đường kính quả bóng. Gọi
V
1
là tổng thể tích ba quả bóng,
V
2
là thể tích của hình trụ. Khi đó tỉ số
V
1
V
2
là A.
1
2...
Đọc tiếp
Người ta bỏ vào một chiếc hộp hình trụ ba quả bóng tennis hình cầu bằng nhau, biết rằng đáy hình trụ bằng hình tròn lớn trên quả bóng, chiều cao của hình trụ gấp 3 lần đường kính quả bóng. Gọi V 1 là tổng thể tích ba quả bóng, V 2 là thể tích của hình trụ. Khi đó tỉ số V 1 V 2 là
A. 1 2
B. 1 4
C. 2 3
D. 3 4