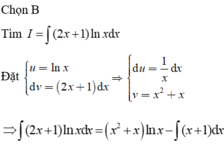Đáp án C

a) F(x) = 1 -  cos x 2 + π 4

d) K(x) = 2 1 - 1 1 + tan x 2

Đáp án C

Ta có  F ' ' x = f ' x = 1 + ln x

\(\int xln\left(x+1\right)dx\)

\(\left\{{}\begin{matrix}u=ln\left(x+1\right)\\dv=xdx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=\dfrac{1}{x+1}dx\\v=\dfrac{x^2}{2}\end{matrix}\right.\)

\(\Rightarrow\int xln\left(x+1\right)dx=\dfrac{x^2}{2}.ln\left(x+1\right)-\int\dfrac{x^2}{2}.\dfrac{1}{x+1}dx=\dfrac{x^2}{2}.ln\left(x+1\right)-\dfrac{1}{2}\int\dfrac{x^2}{x+1}dx\)

Xet \(\int\dfrac{x^2}{x+1}dx=\int\dfrac{\left(x+1\right)\left(x-1\right)}{x+1}dx+\int\dfrac{1}{x+1}dx\)

\(=\int\left(x-1\right)dx+\int\dfrac{1}{x+1}dx\)

\(=\dfrac{x^2}{2}-x+ln\left(x+1\right)\)

\(\Rightarrow\int xln\left(x+1\right)dx=\dfrac{x^2}{2}.ln\left(x+1\right)-\dfrac{1}{2}\left(\dfrac{x^2}{2}-x+ln\left(x+1\right)\right)\)

g: \(y=ln\left(x^2+x+1\right)\)

=>\(y'=\dfrac{\left(x^2+x+1\right)'}{x^2+x+1}=\dfrac{2x+1}{x^2+x+1}\)

l: \(y=\dfrac{lnx}{x+1}\)

=>\(y'=\dfrac{\left(lnx\right)'\cdot\left(x+1\right)-\left(x+1\right)'\left(lnx\right)}{\left(x+1\right)^2}\)

=>\(y'=\dfrac{\dfrac{1}{x}\left(x+1\right)-lnx}{\left(x+1\right)^2}\)

\(\Leftrightarrow y'=\dfrac{\dfrac{\left(x+1\right)}{x}-lnx}{\left(x+1\right)^2}\)

e 2 x 12 4 e x + 6 x - 3 + C

Hướng dẫn: Đặt u = x + e x , dv =  e 2 x dx

xtanx + ln cosx + 1 cosx + C

Hướng dẫn: Đặt u = x + sinx, dv = d(tanx)

sin x - x + 1 cos x + 1 3 cos 3 x + C

Hướng dẫn: Đặt u = x + sin 2 x , dv = sinxdx