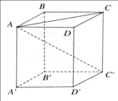
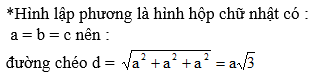Tính độ dài đường chéo của một hình lập phương cạnh a.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Tính độ dài đường chéo của một hình lập phương cạnh a ?
Cho hình lập phương có cạnh bằng a. Tính độ dài đường chéo của hình lập phương đó.
ΔABC vuông tại B
=>\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
ΔA'AC vuông tại A
=>\(A'C=\sqrt{A'A^2+AC^2}=a\sqrt{3}\)
=>Độ dài đường chéo là \(a\sqrt{3}\)
Đúng 1
Bình luận (0)
1) Độ dài một cạnh hình thoi là 20cm, độ dài một đường chéo hình thang là 24cm. Tính diện tích hình thoi
2) Một hình lập phương có thể tích là 125cm3. Tính diện tích xung quanh của hình lập phương
1) Một nữa độ dài đường chéo của hình thôi đã biết: \(\dfrac{24}{2}=12cm\)
Cạnh của hình thôi và một nữa độ dài đường chéo sẽ tạo nên một tam giác vuông tại giao điểm của 2 đường chéo:
Đặt A là một nữa độ dài đường chéo chưa biết.
Áp dụng định lý Pytago ta có:
\(20^2=A^2+12^2\)
\(\Rightarrow A^2=20^2-12^2=256\)
\(\Rightarrow A=\sqrt{256}=16\left(cm\right)\)
Vậy độ dài đường chéo chưa biết là: \(16.2=32\left(cm\right)\)
Diện tích hình thôi là:
\(\dfrac{1}{2}\left(32.24\right)=384\left(cm^2\right)\)
2) Độ dài cạnh của hình lập phương là:
\(\sqrt[3]{125}=5cm\)
Diện tích xung quanh của hình lập phương là:
\(5^2.4=100\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D' có AC = 5cm. Hãy tính:
a) Độ dài cạnh hình lập phương;
b) Độ dài đường chéo hình lập phương;
c) Thể tích hình lập phương.
Độ dài đường chéo AC1 của một hình lập phương là 12 . Độ dài mỗi cạnh là bao nhiêu?
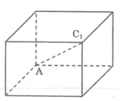
Gọi a là độ dài cạnh của hình lập phương. Vì là hình lập phương nên kích thước các cạnh bằng nhau.
Như vậy đường chéo đáy, là đường chéo hình vuông cạnh ạ.
Độ dài đường chéo đáy là a 2
Suy ra: A C 1 2 = a 2 2 + a 2 = 2 a 2 + a 2 = 3 a 2
Mà AC1 = 12 nên 3 a 2 =12 ⇒ a 2 =4 ⇒ a=2
Vậy cạnh hình lập phương bằng 2(đơn vị dài)
Đúng 0
Bình luận (0)
a) Một hình vuông có cạnh bằng 5cm. Tính độ dài đường chéo của hình vuông.
b) Một hình vuông có độ dài đường chéo bằng 12 cm. Tính độ dài cạnh của hình vuông đó
c) Một hình thoi có độ dài hai đường chéo lần lượt bằng 6cm và 8cm. Tính chu vi của hình thoi đó.
a: Độ dài đường chéo là \(5\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
Một hình chữ nhật có độ dài một cạnh bằng 5cm, độ dài đường chéo bằng 13cm. Tính diện tích hình chữ nhật đó?(Giải bài toán bằng cách lập phương trình)
độ dài cạnh còn lại của HCN :
132- 52=144
=> cạnh còn lại = 12 cm
S hcn :
12 . 5=60 cm
Bài 1. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. a. Tính độ dài đường chéo của hình lập phương. b. Tính góc giữa AC' và mặt đáy c. Tính góc giữa AC và B'C' d. Tính khoảng cách từ A đến (A'BD)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.
a) Tính độ dài đường chéo của hình lập phương.
b) Chứng minh rằng (ACC′A′) \( \bot \) (BDD′B′).
c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng \(\widehat {COC'}\) là một góc phẳng của góc nhị diện [C, BD, C']. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C'], [A, BD, C'].
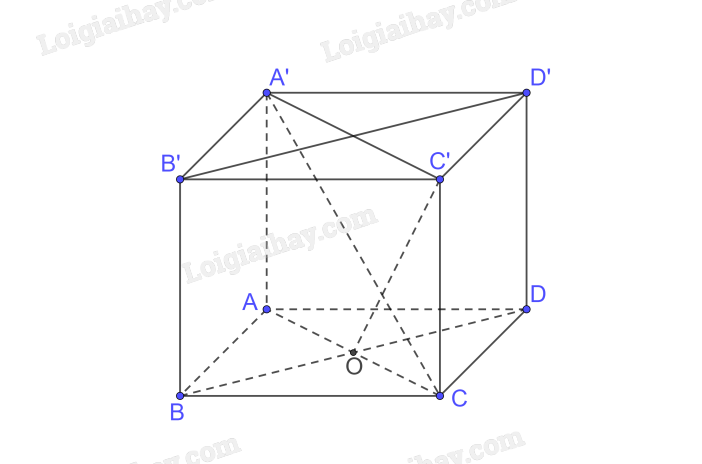
a) Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {a^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác AA’C vuông tại A có
\(A'{C^2} = A{A'^2} + A{C^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow A'C = a\sqrt 3 \)
Vậy độ dài đường chéo hình lập phương bằng \(a\sqrt 3 \)
b) Ta có \(\begin{array}{l}BD \bot AC,BD \bot AA' \Rightarrow BD \bot \left( {ACC'A'} \right);BD \subset \left( {BDD'B'} \right)\\ \Rightarrow \left( {ACC'A'} \right) \bot \left( {BDD'B'} \right)\end{array}\)
c) Ta có \(C'O \bot BD\left( {BD \bot \left( {ACC'A'} \right)} \right),CO \bot BD \Rightarrow \left[ {C,BD,C'} \right] = \left( {CO,C'O} \right) = \widehat {COC'}\)
\(OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác COC’ vuông tại C có
\(\tan \widehat {COC'} = \frac{{CC'}}{{OC}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 \Rightarrow \widehat {COC'} = \arctan \sqrt 2 \)
Ta có \(C'O \bot BD\left( {BD \bot \left( {ACC'A'} \right)} \right),AO \bot BD \Rightarrow \left[ {A,BD,C'} \right] = \left( {AO,C'O} \right) = \widehat {AOC'}\)
\(\widehat {AOC'} = {180^0} - \widehat {COC'} \approx 125,{26^0}\)
Đúng 0
Bình luận (0)