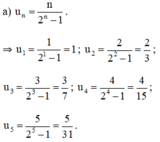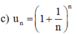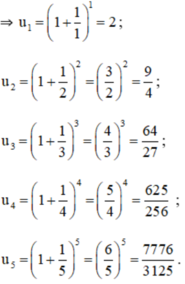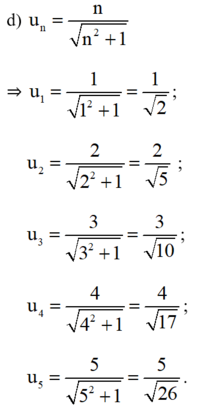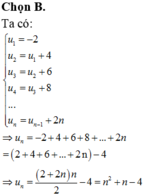Viết năm số hạng đầu của dãy số có số hạng tổng quát un cho bởi công thức: u n = 2 n - 1 2 n + 1
PB
Những câu hỏi liên quan
Viết năm số hạng đầu của dãy số có số hạng tổng quát u n cho bởi công thức: u n = n n 2 - 1
Viết năm số hạng đầu của dãy số có số hạng tổng quát un cho bởi công thức: u n = 1 + 1 n n
Viết năm số hạng đầu của dãy số có số hạng tổng quát u n cho bởi công thức: u n = 1 n 2 + 1
Dãy số
u
n
cho bởi
u
1
3
,
u
n
+
1
1
+
u
n
2
,
n
1...
Đọc tiếp
Dãy số u n cho bởi u 1 = 3 , u n + 1 = 1 + u n 2 , n > 1
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.
a. Năm số hạng đầu của dãy số
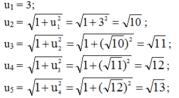
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
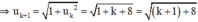
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.
Đúng 0
Bình luận (0)
Dãy số \(\left( {{u_n}} \right)\)cho bởi hệ thức truy hồi: \({u_1} = 1,\;\;\;{u_n} = n.{u_{n - 1}}\) với \(n \ge 2\)
a) Viết năm số hạng đầu của dãy số.
b) Dự đoán công thức số hạng tổng quát \({u_n}\).
a) \({u_1} = 1\)
\( \Rightarrow {u_2} = 2.1 = 2\)
\( \Rightarrow {u_3} = 3.2 = 6\)
\( \Rightarrow {u_4} = 4.6 = 24\)
\( \Rightarrow {u_5} = 5.24 = 120\)
b)
Ta có:
\({u_2} = 2 = 2.1 \)
\({u_3} = 6= 1.2.3 \)
\({u_4} = 24 = 1.2.3.4\)
\({u_5} = 120 = 1.2.3.4.5\)
\( \Rightarrow {u_n} = 1.2.3....n = n!\).
Đúng 0
Bình luận (0)
Cho dãy số (un)(��) biết : u1−1;un+1un+3�1−1;��+1��+3 với n≥1�≥1Viết năm số hạng đầu và tìm công thức tính số hạng tổng quát un theo n
Đọc tiếp
Cho dãy số biết :
với
Viết năm số hạng đầu và tìm công thức tính số hạng tổng quát un theo n
u1=-1
u2=-1+3=2
u3=2+3=5
u4=5+3=8
u5=8+3=11
Công thức tổng quát là: \(U_n=U_1+\left(n-1\right)\cdot\left(3\right)=-1+3n-3=3n-4\)
Đúng 1
Bình luận (0)
Cho dãy số (Un) xác định bởi công thức truy hồi:
u
1
-
2
u
n
u
n
-
1...
Đọc tiếp
Cho dãy số (Un) xác định bởi công thức truy hồi: u 1 = - 2 u n = u n - 1 + 2 n , ∀ n ≥ 2 , n ∈ N * . Tìm số hạng tổng quát của dãy số
![]()
![]()
![]()
![]()
Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát \({u_n}\) cho bởi công thức sau:
a) \({u_n} = 2{n^2} + 1\)
b) \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{2n - 1}}\)
c) \({u_n} = \frac{{{2^n}}}{n}\)
d) \({u_n} = {\left( {1 + \frac{1}{n}} \right)^n}\)
a) Năm số hạng đầu của dãy số là: 3; 9; 19; 33; 51
b) Năm số hạng đầu của dãy số là: \( - 1;\frac{1}{3}; - \frac{1}{5};\frac{1}{7}; - \frac{1}{9}\)
c) Năm số hạng đầu của dãy số là: \(2;2;\frac{8}{3};4;\frac{{32}}{5}\)
d) Năm số hạng đầu của dãy số là: \(2;\frac{9}{4};\frac{{64}}{{27}};\frac{{625}}{{256}};\frac{{7776}}{{3125}}\)
Đúng 0
Bình luận (0)
Cho dãy số (un) = n2.
a) Viết năm số hạng đầu và số hạng tổng quát của dãy số (un).
b) Viết dạng khai triển của dãy số (un).
a) Năm số hạng đầu của dãy số là: \(u_1=1^2=1;u_2=2^2=4;u_3=3^2=9;u_4=4^2=16;u_5=5^2=25\).
Số hạng tổng quát của dãy số un là \(u_n=n^2\) với n ∈ ℕ.
b) Dạng khai triển của dãy số \(u_1=1,u_2=4,u_3=9,u_4=16,...u_n=n^2\) ...
Đúng 0
Bình luận (0)