Tâm đối xứng I của đồ thị hàm số y = − 2 x − 1 x + 1 là
A. I 1 ; − 2
B. I − 1 ; − 2
C. I 1 ; 2
D. I − 1 ; 2
PB
Những câu hỏi liên quan
Cho hàm số
y
x
-
1
x
+
m
,
m
≠
-
1
, có đồ thị (C). Tìm m để...
Đọc tiếp
Cho hàm số y = x - 1 x + m , m ≠ - 1 , có đồ thị (C). Tìm m để đồ thị (C) nhận I (2;) làm tâm đối xứng.
A. m = 1 2
B. m = - 1 2
C. m = 2
D. m = -2
Chọn: D
Đồ thị (C) nhận I (2;1) làm tâm đối xứng
Đúng 0
Bình luận (0)
Tâm đối xứng của đồ thị hàm số y = 1 + 4 x 1 + x là
A. I(4;-1)
B. I(-1;1)
C. I(4;1)
D. I(-1;4)
Đáp án là D
Tiệm cận đứng của đồ thị là x= -1.
Tiệm cận ngang của đồ thị là y = 4.
=> Tâm đối xứng của đồ thị hàm số
y = 1 + 4 x 1 + x là I(-1;4).
Nhận xét: đồ thị hàm số y = a x + b c x + d có tâm đối xứng là giao điểm hai đường tiệm cận đứng và tiệm cận ngang.
Đúng 0
Bình luận (0)
Tọa độ tâm đối xứng của đồ thị hàm số
y
x
-
2
2
x
-
1
là A.
-
1
2
;
2
B.
1
2
;...
Đọc tiếp
Tọa độ tâm đối xứng của đồ thị hàm số y = x - 2 2 x - 1 là
A. - 1 2 ; 2
B. 1 2 ; 1 2
C. 1 2 ; - 1
D. - 1 2 ; 1 2
Chọn B.
Tâm đối xứng của đồ thị hàm số này là giao điểm của 2 đường tiệm cận 1 2 ; 1 2
Đúng 0
Bình luận (0)
Tìm tọa độ tâm đối xứng của đồ thị hàm số y=(2x+1)/(x-1)
A. (1;2)
B. (2;1)
C. (1;-1)
D. (-1;1)
Quan sát đồ thị hàm số y sin x ở Hình 25.a) Nêu tập giá trị của hàm số y sin xb) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y sin xc) Bằng cách dịch chuyển đồ thị hàm số y sin x trên đoạn left[ { - pi ;pi } right] song song với trục hoành sang phải theo đoạn có độ dài 2pi , ta có nhận được đồ thị hàm số y sin x trên đoạn left[ {pi ;3pi } right] hay không? Hàm số y sin xcó tuần hoàn hay không/d) Tìm khoảng đồng biến, nghịch...
Đọc tiếp
Quan sát đồ thị hàm số \(y = \sin x\) ở Hình 25.
a) Nêu tập giá trị của hàm số \(y = \sin x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \sin x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta có nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \sin x\)có tuần hoàn hay không/
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \sin x\)
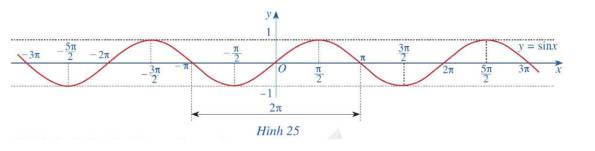
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)
Đúng 0
Bình luận (0)
Quan sát đồ thị hàm số y cot x ở Hình 32.a) Nêu tập giá trị của hàm số y cot xb) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y cot xc) Bằng cách dịch chuyển đồ thị hàm số y cot x trên khoảng left( {0;pi } right) song song với trục hoành sang phải theo đoạn có độ dài pi , ta nhận được y cot x trên khoảng left( {pi ;2pi } right) hay không? Hàm số y cot x có tuần hoàn hay không?d) Tìm khoảng đồng biến, nghịch biến của hàm số y...
Đọc tiếp
Quan sát đồ thị hàm số \(y = \cot x\) ở Hình 32.
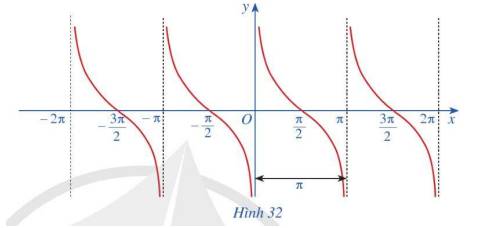
a) Nêu tập giá trị của hàm số \(y = \cot x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \cot x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\) hay không? Hàm số \(y = \cot x\) có tuần hoàn hay không?
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \cot x\)
a) Tập giá trị của hàm số \(y = \cot x\)là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Hàm số \(y = \cot x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\)
Hàm số \(y = \cot x\) có tuần hoàn
d) Hàm số \(y = \cot x\)nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right),k \in Z\)
Đúng 0
Bình luận (0)
Quan sát đồ thị hàm số y tan x ở Hình 30a) Nêu tập giá trị của hàm số y tan xb) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số hay không? Từ đó kết luận tính chẵn, lẻ của hàm số y tan xc) Bằng cách dịch chuyển đồ thị hàm số y tan x trên khoảng left( { - frac{pi }{2};frac{pi }{2}} right) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số y tan x trên khoảng left( {frac{pi }{2};frac{{3pi }}{2}} right) hay không? Hàm số y tan x có tuần hoàn hay k...
Đọc tiếp
Quan sát đồ thị hàm số \(y = \tan x\) ở Hình 30
a) Nêu tập giá trị của hàm số \(y = \tan x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số hay không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \tan x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\) hay không? Hàm số \(y = \tan x\) có tuần hoàn hay không?
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \tan x\)
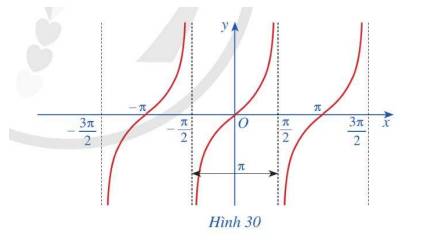
a) Tập giá trị của hàm số \(y = \tan x\) là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Như vậy, hàm số \(y = \tan x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
Như vậy, hàm số \(y = \tan x\) có tuần hoàn
d) Hàm số \(y = \tan x\)đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) với \(k \in Z\)
Đúng 0
Bình luận (0)
Đồ thị hàm số y f(x) đối xứng với đồ thị của hàm số
y
a
x
(
a
0
,
a
≠
1
)
qua điểm I(1;1). Giá trị của biểu thức
2
+
log
a
1
2018
bằng
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị của hàm số y = a x ( a > 0 , a ≠ 1 ) qua điểm I(1;1). Giá trị của biểu thức 2 + log a 1 2018 bằng
Đồ thị hàm số y f(x) đối xứng với đồ thị hàm số
y
log
a
x
(
0
a
≠
1
)
qua điểm I(2; 1). Giá trị của biểu thức
f
(
4
-
a
2019
)
bằng A. 2023 B. -2023 C. 2017 D. -2017
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số y = log a x ( 0 < a ≠ 1 ) qua điểm I(2; 1). Giá trị của biểu thức f ( 4 - a 2019 ) bằng
A. 2023
B. -2023
C. 2017
D. -2017
