Chọn: D
Đồ thị (C) nhận I (2;1) làm tâm đối xứng
![]()
Chọn: D
Đồ thị (C) nhận I (2;1) làm tâm đối xứng
![]()
Cho hàm số y = a x 3 + b x 2 + c x + d . Biết rằng đồ thị hàm số có một điểm cực trị là M(1;-1) và nhận I(0;1) làm tâm đối xứng. Giá trị y(2) là:
A. y(2) = 2
B. y(2) = -2
C. y(2) = 6
D. y(2) = 3
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Tìm m để đồ thị hàm số y = a x + 1 2 x - b nhận điểm I(1;1) làm tâm đối xứng
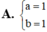
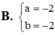
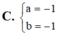
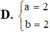
Cho hàm số \(y=\dfrac{1}{2}x^4-x^2+m\)(m là tham số ) có đồ thị (Cm), đường tròn (S)có phương trình \(x^2+y^2+2x+6y+1=0\) và điểm A(-1;-6).Tìm m để tồn tại tiếp tuyến với đồ thị (Cm) cắt đường tròn (S) tại hai điểm phân biệt B,C sao cho tam giác ABC có chu vi đạt giá trị lớn nhất
Cho hàm số y = x x - 1 có đồ thị (C) .Gọi ∆ là tiếp tuyến tại điểm M(x0; y0) (với x0 > 0) thuộc đồ thị (C). Để khoảng cách từ tâm đối xứng I của đồ thị (C) đến tiếp tuyến là lớn nhất thì tung độ của điểm M gần giá trị nào nhất?
A. 7 π 2
B. 3 π 2
C. 5 π 2
D. π 2
Cho hàm số có đồ thị (C) y = 2 x + 1 x - 1 và đường thẳng d: y=x+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là
A.m=1
B.m=1 hoặc m=5
C.m=5
D.m=-5
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3-3( m+1) x2+ 12mx-3m+ 4 ( C) có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm C(-1; -9/2) lập thành tam giác nhận gốc tọa độ làm trọng tâm.
A. m= -1/2
B. m= -2
C. m=2
D. m =1/2
cho hàm số y=X4-2mx2+m(C) với m là tham số thực.Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1.tìm tham số m để tiếp tuyến đenta với đồ thị (C) tại A cắt đường tròn (T): x2+(y-1)2=4 tạo thành dây cung có độ dài nhỏ nhất
A.m=16/13
B.-13/16
C.13/16
D.-16/13
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()