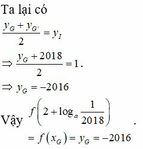Các câu hỏi tương tự
Đồ thị hàm số y f(x) đối xứng với đồ thị hàm số
y
log
a
x
(
0
a
≠
1
)
qua điểm I(2; 1). Giá trị của biểu thức
f
(
4
-
a
2019
)
bằng A. 2023 B. -2023 C. 2017 D. -2017
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số y = log a x ( 0 < a ≠ 1 ) qua điểm I(2; 1). Giá trị của biểu thức f ( 4 - a 2019 ) bằng
A. 2023
B. -2023
C. 2017
D. -2017
Đồ thị hàm số y f(x) đối xứng với đồ thị hàm số
y
log
a
x
;
(
0
a
≠
1
)
qua điểm I(2;1). Giá trị của biểu thức
f
(
4
-
a
2019
)
bằng A. 2023 B. -2023 C. 2017 D. -2017
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số y = log a x ; ( 0 < a ≠ 1 ) qua điểm I(2;1). Giá trị của biểu thức f ( 4 - a 2019 ) bằng
A. 2023
B. -2023
C. 2017
D. -2017
Đồ thị hàm số
y
f
(
x
)
đối xứng với đồ thị hàm số
y
log
a
x
;
(
0
a
≠
1
)
qua điểm
I
2
;
1
. Giá trị của biểu thức
f
4
-
a...
Đọc tiếp
Đồ thị hàm số y = f ( x ) đối xứng với đồ thị hàm số y = log a x ; ( 0 < a ≠ 1 ) qua điểm I 2 ; 1 . Giá trị của biểu thức f 4 - a 2019 bằng
A. 2023
B. -2023
C. 2017
D. -2017
Biết hai hàm số
y
a
x
,
y
f
(
x
)
có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng
y
-
x
. Tính
f
-
a
+
f
-
a
2
A. -3 B. 4 C....
Đọc tiếp
Biết hai hàm số y = a x , y = f ( x ) có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng y = - x . Tính f - a + f - a 2
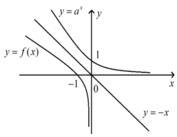
A. -3
B. 4
C. 5
D. đáp án khác
Biết hai hàm số
y
a
x
;
y
f
(
x
)
có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng y -x. Tính
f
(
-
a
)
+
f
(
-
a
2
)
A. -3 B. 4 C. 5 D. 3
Đọc tiếp
Biết hai hàm số y = a x ; y = f ( x ) có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng y = -x. Tính f ( - a ) + f ( - a 2 )
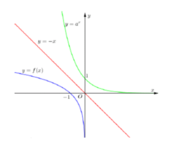
A. -3
B. 4
C. 5
D. 3
Cho hàm số y
x
+
1
x
-
1
có đồ thị (C) biết cả hai đường thẳng
d
1
:
y
a
1
x
+
b
1
;
d
2
:
a...
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị (C) biết cả hai đường thẳng d 1 : y = a 1 x + b 1 ; d 2 : a 2 x + b 2 đi qua điểm I(1;1) và cắt đồ thị (C) tại 4 điểm tạo thành một hình chữ nhật. Khi a 1 + a 2 = 5 2 ,giá trị biểu thức bằng:
![]()
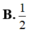
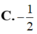
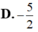
Cho hàm số y -x3+3mx2-3m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng d: x+8y-740. A. m1 B. m- 2 C. m -1 D. m1
Đọc tiếp
Cho hàm số y= -x3+3mx2-3m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng d: x+8y-74=0.
A. m=1
B. m=- 2
C. m= -1
D. m=1
Cho hàm số y f( x) ax4+ bx2+ c ( a 0) có đồ thị (C), đồ thị hàm số y f’(x). Đồ thị hàm số y f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành? A.
7
15
B.
8
15
C.
14
15
D.
16
15
Đọc tiếp
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
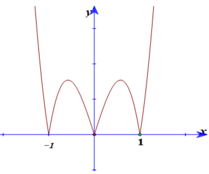
A. 7 15
B. 8 15
C. 14 15
D. 16 15
Gọi (C) là đồ thị của hàm số
y
lo
2018
x
và
C
là đồ thị của hàm số y f(x) ,
C
đối xứng với (C) qua trục tung. Hàm số
y
f
x
đồng biến trên khoảng nào sau đây?
Đọc tiếp
Gọi (C) là đồ thị của hàm số y = lo 2018 x và C ' là đồ thị của hàm số y = f(x) , C ' đối xứng với (C) qua trục tung. Hàm số y = f x đồng biến trên khoảng nào sau đây?
![]()
![]()
![]()
![]()