Cho hình bình hành ABCD với A − 2 ; 3 ; 1 , B 3 ; 0 ; − 1 , C 6 ; 5 ; 0 . Tọa độ đỉnh D là
A. D(1;8;-2)
B. D(11;2;2)
C. D(1;8;2)
D. D(11;2;-2)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình bình hành ABCD với A(2;3;-2), B(1;1;-3), C(-2;0;5), D(-1;3;4). Diện tích của hình bình hành ABCD bằng:
![]()
![]()
![]()
![]()
Cho hình bình hành ABCD với A(2; 4; -2), B(1; 1; -3), C(-2; 0; 5), D(-1; 3; 4). Diện tích của hình bình hành ABCD bằng:
A. 245 đvdt
B. 615 đvdt
C. 2 731 đvdt
D. 345 đvdt
Cho hình bình hành ABCD có AB = 6cm, BC = 10cm. Tính diện tích hình bình hành ABCD biết chiều cao tương ứng với đáy AB bằng trung bình cộng của 2 cạnh bên hình bình hành
Chiều cao là \(\dfrac{10+10}{2}=10\left(cm\right)\)
Diện tích hbh là \(10\cdot6=60\left(cm^2\right)\)
mn ơi giuos mik ik
mik đang gấp ạ
xin cảm ơn
Cho hình bình hành ABCD có BD vuông góc với BC. Biết AB=a, góc A = α . Tính diện tích hình bình hành ABCD theo a và α
Cho hình bình hành ABCD O là giao điểm của 2 đường chéo. Vẽ AH và CK vuông góc với BD. a) cm tứ giác AHCK là hình bình hành.
Lời giải:
Vì $ABCD$ là hình bình hành nên $AO=OC$
Xét tam giác $AHO$ và $CKO$ có:
$\widehat{AHO}=\widehat{CKO}=90^0$
$\widehat{AOH}=\widehat{COK}$ (đối đỉnh)
$AO=CO$
$\Rightarrow \triangle AHO=\triangle CKO$ (ch-gn)
$\Rightarrow AH=CK$
Tứ giác $AHCK$ có 2 cạnh đối $AH, CK$ song song (do cùng vg với $BD$) và bằng nhau nên $AHCK$ là hbh.
Bài 1: Cho hình bình hành ABCD , đường chéo BD . Kẻ AH và CK vuông góc với BD tại H và K . Chứng minh tứ giác AHCK là hình bình hành. Bài 2: Cho hình bình hành ABCD có M N, lần lượt là trung điểm của AB CD , . AN và CM cắt BD lần lượt tại E và F . a) Chứng minh AMCN là hình bình hành. ( Hình 6) b) Từ F kẻ đường thẳng song song với AB cắt AN tại G. Chứng minh BF FE ED . Bài 3: Cho tam giác ABC cân tại A , lấy điểm D trên cạnh AB , điểm E trên cạnh AC sao cho BD CE . a) Tứ giác BDEC là hì gì? Vì sao? b) Các điểm D E, ở vị trí nào thì BD DE EC
Bài 3:
a: Ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
Hình thang BDEC có \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
b: Để BD=DE=EC thì BD=DE và DE=EC
BD=DE thì ΔDBE cân tại D
=>\(\widehat{DBE}=\widehat{DEB}\)
mà \(\widehat{DEB}=\widehat{EBC}\)(hai góc so le trong, DE//BC)
nên \(\widehat{DBE}=\widehat{EBC}\)
=>\(\widehat{ABE}=\widehat{EBC}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC
Xét ΔEDC có ED=EC
nên ΔEDC cân tại E
=>\(\widehat{EDC}=\widehat{ECD}\)
mà \(\widehat{EDC}=\widehat{DCB}\)(hai góc so le trong, DE//BC)
nên \(\widehat{ECD}=\widehat{DCB}\)
=>\(\widehat{ACD}=\widehat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác từ C kẻ xuống AB
Bài 2:
a: Ta có: ABCD là hình bình hành
=>AB//CD và AB=CD(1)
Ta có: M là trung điểm của AB
=>\(AM=MB=\dfrac{AB}{2}\left(2\right)\)
Ta có: N là trung điểm của CD
=>\(NC=ND=\dfrac{CD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AM=MB=NC=ND
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Ta có AMCN là hình bình hành
=>AN//CM
Xét ΔDFC có
N là trung điểm của DC
NE//FC
Do đó: E là trung điểm của DF
=>DE=EF(4)
Xét ΔABE có
M là trung điểm của BA
MF//AE
Do đó: F là trung điểm của BE
=>BF=FE(5)
Từ (4) và (5) suy ra BF=FE=ED
Trong không gian với hệ tọa độ Oxyz cho hình bình hành ABCD. Biết A(2;1;-3), B(0;-2;5) và C(1;1;3). Diện tích hình bình hành ABCD là
A. 2 87
B. 349 2
C. 349
D. 87
Đáp án C
Giả sử D(a;b;c).Vì ABCD là hình bình hành nên
![]()
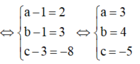
![]()
Diện tích hình bình hành ABCD là
![]()
Đúng ghi Đ, sai ghi S
Hình bình hành ABCD (hình bên) có
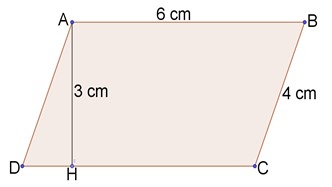
a, AB vuông góc với DC
b, AH vuông góc với DC
c, Chu vi hình bình hành ABCD là 18 cm
d, Diện tích hình bình hành ABCD là 18 c m 2
Cho hình bình hành ABCD có AB = 6cm, BC = 10cm. Tính diện tích hình bình hành ABCD biết chiều cao tương ứng với đáy AB bằng trung bình cộng của 2 cạnh bên hình bình hành
mn ơi giuos mik vói ạ
đúng tick nha
Cho hình bình hành ABCD biết BD vuông góc với BC, AB = a, góc A = alpha. Tính S hình bình hành theo a và alpha
Ta có: BD=AB.sinA=a.sin(alpha)
AD=AB.cosA=a.cos(alpha)
=>S=2SABD
=BD.AD=a2.sin(alpha).cos(alpha)