Gọi m 0 là giá trị thực của tham số m để đồ thị hàm số y = x 4 + 2 m x 2 + 4 có 3 điểm cực trị nằm trên các trục tọa độ. Khẳng định nào sau đây là đúng?
A. m 0 ∈ 1 ; 3
B. m 0 ∈ − 5 ; − 3
C. m 0 ∈ − 3 2 ; 0
D. m 0 ∈ − 3 ; − 3 2
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Đầu tiên, ta cần tìm điểm cực trị của hàm số f(x) = x^3 - 3x^2 + m. Điều kiện cần và đủ để x_0 là điểm cực trị của hàm số y = f(x) là f’(x_0) = 0 và f’'(x_0) ≠ 0.
Ta có f’(x) = 3x^2 - 6x và f’'(x) = 6x - 6.
Giải phương trình f’(x) = 0, ta được x_1 = 0 và x_2 = 2. Kiểm tra điều kiện thứ hai, ta thấy f’‘(0) = -6 ≠ 0 và f’'(2) = 6 ≠ 0 nên x_1 = 0 và x_2 = 2 là hai điểm cực trị của hàm số.
Vậy, A = (0, f(0)) = (0, m) và B = (2, f(2)) = (2, 4 - m).
Trọng tâm G của tam giác OAB có tọa độ (x_G, y_G) = (1/3 * (x_A + x_B + x_O), 1/3 * (y_A + y_B + y_O)) = (2/3, 1/3 * (m + 4)).
Để G thuộc đường thẳng 3x + 3y - 8 = 0, ta cần có 3 * (2/3) + 3 * (1/3 * (m + 4)) - 8 = 0. Giải phương trình này, ta được m = 2.
Vậy, đáp án là B. m = 2.
Cho hàm số y = \(\dfrac{\left(3m+1\right)x-m^2+m}{x+m}\) trong đó m là tham số khác 0. Gọi S là tập hợp các giá trị thực của m để tại giao điểm của đồ thị với trục hoành, tiếp tuyến sẽ vuông góc với đường thẳng x+y-2020 = 0. Khi đó tổng giá trị các phần tử thuộc S bằng
Tiếp tuyến có hệ số góc bằng 1
\(y'=\dfrac{m\left(3m+1\right)-\left(-m^2+m\right)}{\left(x+m\right)^2}=\dfrac{4m^2}{\left(x+m\right)^2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\dfrac{4m^2}{\left(x+m\right)^2}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}2m=x+m\\-2m=x+m\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}x=m\\x=-3m\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\dfrac{m^2-m}{3m+1}\\-3m=\dfrac{m^2-m}{3m+1}\end{matrix}\right.\)
\(\Leftrightarrow...\)
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Cho hàm số f ( x ) = x 3 + m x 2 + x + 1 Gọi k là hệ số góc tiếp tuyến của đồ thị hàm số tại M có hoành độ x = 1. Tất cả các giá trị thực của tham số m để thỏa mãn k.f(-1)<0
![]()
![]()
![]()
![]()
Cho hàm số y= x3-3x2-mx+2 với m là tham số thực. Tìm giá trị của m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng d ; x+4y-5=0 một góc α = 45 ° .
A. m= -1/2
B. m= 1/2
C. m=0
D. m= 1
Ta có y’=3x2-6x-m
Để đồ thị hàm số đã cho có hai điểm cực trị khi phương trình y’=0 có hai nghiệm phân biệt ⇔ ∆ ' = 9 + 3 m > 0 ⇔ m > - 3
Ta có 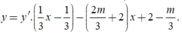
đường thẳng đi qua hai điểm cực trị Avà B là 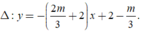
Đường thẳng d; x+4y-5=0 có một VTPT là n d → = ( 1 ; 4 ) .
Đường thẳng 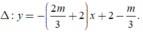 có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
Ycbt suy ra:
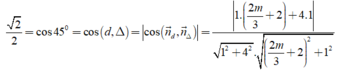
Suy ra
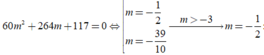 thỏa mãn
thỏa mãn
Chọn A.
Cho hàm số y= x3- 3mx2+4m2-2 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có hai điểm cực trị A; B sao cho I( 1; 0) là trung điểm của đoạn thẳng AB.
A. 0
B. -1.
C. 1.
D. 2.
Ta có 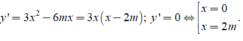
Đề đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó tọa độ hai điểm cực trị là A( 0 ; 4m2- 2) và B( 2m; 4m2- 4m3-2).
Do I( 1; 0) là trung điểm của AB nên
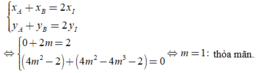
Chọn C.
Cho hàm số y= -x3+3mx2-3m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng d: x+8y-74=0.
A. m=1
B. m=- 2
C. m= -1
D. m=1
Ta có 
Để đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó gọi A( 0 ; -3m-1) và B( 2m ; 4m3-3m-1) là hai điểm cực trị của đồ thị hàm số.
Suy ra trung điểm của AB là điểm I ( m ; 2m3-3m-1) và A B → = ( 2 m ; 4 m 3 ) = 2 m ( 1 ; 2 m 2 )
Đường thẳng d có một vectơ chỉ phương là u → = ( 8 ; - 1 ) .
Ycbt 
Chọn D.
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
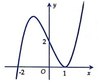
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > − 1
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
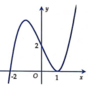
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > 1
Đáp án B.
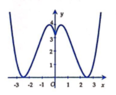
Hàm số y = f x + m là một hàm số chẵn nên đồ thị đối xứng qua trục Oy. Mặt khác y = f x + m = f x + m ∀ x ≥ 0 . Ta có phép biến đổi từ đồ thị hàm số y = f x thành đồ thị hàm số y = f x + m :
* Nếu m > 0:
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang trái m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
* Nếu m=0 :
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang phải m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
Quan sát ta thấy đồ thị hàm số y = f x có 2 điểm cực trị.
Để đồ thị hàm số y = x + m có 5 điểm cực trị thì nhánh bên phải Oy của đồ thị hàm số y = x + m phải có 2 điểm cực trị => Điểm cực trị của đồ thị hàm số y = f x phải được tịnh tiến sang phải O y ⇒ m < − 1 .
Cho hàm số y = x - m 2 x + 1 (với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?
A. Hai.
B. Ba.
C. Một.
D. Không