Cho 0 < a < 1 , b > 1 và M = log a 2 , N = log 2 b . Khi đó khẳng định nào sau đây đúng?
A. M >0 và N > 0
B. M >0 và N < 0
C. M <0 và N < 0
D. M <0 và N > 0
Nếu \({a^{\frac{1}{2}}} = b\left( {a > 0,a \ne 1} \right)\) thì
A. \({\log _{\frac{1}{2}}}a = b\).
B. \(2{\log _a}b = 1\).
C. \({\log _a}\frac{1}{2} = b\).
D. \({\log _{\frac{1}{2}}}b = a\).
\({a^{\frac{1}{2}}} = b \Leftrightarrow {\log _a}b = \frac{1}{2} \Leftrightarrow 2{\log _a}b = 1\)
Chọn B.
Hoạt động 4
Cho \(a > 0;a \ne 1;b > 0\), α là một số thực
a) Tính \({a^{{{\log }_a}{b^\alpha }}}\,\,\,và \,\,\,{a^{\alpha {{\log }_a}b}}\)
b) So sánh \({\log _a}{b^\alpha }\,\,\,và \,\,\,\alpha {\log _a}b\)
\(a,a^{log_ab^{\alpha}}=c\Leftrightarrow log_ac=log_ab^{\alpha}\Leftrightarrow c=b^{\alpha}\Rightarrow a^{log_ab^{\alpha}}=b^{\alpha}\\ a^{\alpha log_ab}=c\Leftrightarrow\alpha log_ab=log_ac\Leftrightarrow log_ab^{\alpha}=log_ac\Leftrightarrow b^{\alpha}=c\Rightarrow a^{\alpha log_ab}=b^{\alpha}\\ \Rightarrow a^{log_ab^{\alpha}}=a^{\alpha log_ab}\)
\(b,a^{log_ab^{\alpha}}=a^{\alpha log_ab}\\ \Rightarrow log_ab^{\alpha}=\alpha log_ab\)
cho a, b>0, và a2 +4b2 =23ab. cmr với 0<c≠1 ta có: logc \(\dfrac{a+2b}{3}\) =\(\dfrac{1}{2}\) (logca+logcb+logc3)
\(a^2+4b^2=23ab\Rightarrow a^2+4ab+4b^2=27ab\Rightarrow\left(a+2b\right)^2=27ab\)
\(\Rightarrow\dfrac{\left(a+2b\right)^2}{9}=3ab\)\(\Rightarrow\left(\dfrac{a+2b}{3}\right)^2=3ab\)
Lấy logarit cơ số c hai vế:
\(log_c\left(\dfrac{a+2b}{3}\right)^2=log_c\left(3ab\right)\)
\(\Rightarrow2log_c\dfrac{a+2b}{3}=log_c3+log_ca+log_cb\)
\(\Rightarrow log_c\dfrac{a+2b}{3}=\dfrac{1}{2}\left(log_ca+log_cb+log_c3\right)\)
Hoạt động 2
Cho \(a > 0;a \ne 1\). Tình:
a) \({\log _a}1\)
b) \({\log _a}a\)
c) \({\log _a}{a^c}\)
d) \({a^{{{\log }_a}b}}\,\,\,(b > 0)\)
\(a,log_a1=c\Leftrightarrow a^c=1\Leftrightarrow c=0\Rightarrow log_a1=0\\ b,log_aa=c\Leftrightarrow a^c=a\Leftrightarrow c=1\Rightarrow log_aa=1\\ c,log_aa^c=b\Leftrightarrow a^b=a^c\Leftrightarrow b=c\Rightarrow log_aa^c=c\\ d,a^{log_ab}=c\Leftrightarrow log_ab=log_ac\Leftrightarrow b=c\Rightarrow a^{log_ab}=b\)
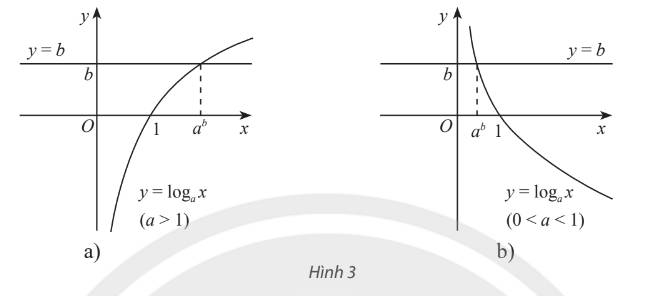
Cho đồ thị của hai hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) và \(y = b\) như Hình 3a (với \(a > 1\)) hay Hình 3b (với \(0 < a < 1\)). Từ đây hãy nhận xét về số nghiệm và công thức nghiệm của phương trình \({\log _a}x = b\).
tham khảo.
Đồ thị của hai hàm số \(y=\log_ax\) và \(y=b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \(\log_ax=b\) có nghiệm duy nhất \(x=a^b\).
1) Cho a,b là các số thực dương khác 1 và thoả mãn ab khác 1. Rút gọn biểu thức sau: P=(logab + logba + 2)(logab - logabb).logba - 1
Cho các số thực dương a, b với a≠1 và log a b >0. Khẳng định nào sau đây là đúng?
A. 0 < a , b < 1 0 < a < 1 < b
B. 0 < a , b < 1 1 < a , b
C. 0 < a , b < 1 0 < b < 1 < a
D. 0 < b < 1 < a 1 < a , b
Cho \(0 < a \ne 1\). Tính giá trị của biểu thức \(B = {\log _a}\left( {\frac{{{a^2} \cdot \sqrt[3]{a} \cdot \sqrt[5]{{{a^4}}}}}{{\sqrt[4]{a}}}} \right) + {a^{2{{\log }_a}\frac{{\sqrt {105} }}{{30}}}}\).
\(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}=\dfrac{a^2\cdot a^{\dfrac{1}{3}}\cdot a^{\dfrac{4}{5}}}{a^{\dfrac{1}{4}}}=\dfrac{a^{\dfrac{47}{15}}}{a^{\dfrac{1}{4}}}=a^{\dfrac{173}{60}}\)
\(\Rightarrow log_a\left(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}\right)=log_a\left(a^{\dfrac{173}{60}}\right)=\dfrac{173}{60}\)
\(a^{2log_a\left(\dfrac{\sqrt{105}}{30}\right)}=a^{log_a\left(\dfrac{7}{60}\right)}=\dfrac{7}{60}\)
Vậy \(B=\dfrac{173}{60}+\dfrac{7}{60}=\dfrac{180}{60}=3\)
Nếu log cơ số a của x=1/2 log cơ số a của 9 -log cơ số a của 5+ log cơ số a của 2 ( a>0. a#1) thì x =?
Cho x ϵ (0;π/2). Biết log(sinx)+log(cosx)=-1 và log(sinx+cosx)=1/2(logn-1). Giá trị của n là
A. 11.
B. 12.
C. 10.
D. 15.