Gọi x và y là các số thực dương thỏa mãn điều kiện l o g 9 x = l o g 6 y = l o g 4 ( x + y ) và x y = - a + b 2 với a, b là hai số nguyên dương. Tính T = a + b
A. T = 6
B. T = 4
C. T = 11
D. T = 8
Gọi x, y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 , với a, b là hai số nguyên dương. Tính a.b.
![]()
![]()
![]()
![]()
Gọi x,y là các số thực dương thỏa mãn điều kiện l o g 9 x = l o g 6 y = l o g 4 ( x + y ) và x y = - a + b 2 , với a,b là hai số nguyên dương. Tính a.b
A. a.b=5
B. a.b=1
C. a.b=8
D. a.b=4
Gọi x và y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 với a, b là hai số nguyên dương. Tính T = a + b
A. T=6
B. T=4
C. T=11
D. T=8
Gọi x, y là các số thực dương thỏa mãn điều kiện log9 x = log6 x = log4 (x + y) và biết rằng x y = - a + b 2 với a, b là các số nguyên dương. Tính giá trị a + b.
A. a + b = 6
B. a + b = 11
C. a + b = 4
D. a + b = 8
Gọi x, y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 x = log 4 x + y và biết rằng x y = - a + b 2 với a, b là các số nguyên dương. Tính giá trị a + b
A. a + b = 6
B. a + b = 11
C. a + b = 4
D. a + b = 8
Đáp án A
Ta có log 9 x = log 6 x = log 4 x + y = t ⇔ x = 9 t y = 6 t ; x + y = 4 t
Khi đó 9 t + 6 t = 4 t ⇔ 3 2 t 2 + 3 2 t - 1 = 0 ⇔ x y = 3 2 t = - 1 + 5 2 ⇒ a = 1 b = 5 .
Bài 1 :Cho 2 số dương x,y thỏa mãn điều kiện \(x+y\le1\). Chứng minh\(x^2-\frac{3}{4x}-\frac{x}{y}\le\frac{-9}{4}\)
Bài 2 : Cho 2 số thực x,y thay đổi thỏa mãn điều kiện x+y\(\ge1\)và x>0
Tìm giá trị nhỏ nhất của biểu thức \(M=y^2+\frac{8x^2+y}{4x}\)
bài 3: cho 3 số dương x,y,z thay đổi luôn thỏa mãn điều kiện x+y+z=1. Tìm giá trị lớn nhất của biểu thức:\(P=\dfrac{x}{x+1}+\dfrac{y}{y+1}+\dfrac{z}{z+1}\)
3: \(P=\dfrac{x}{\left(x+y\right)+\left(x+z\right)}+\dfrac{y}{\left(y+z\right)+\left(y+x\right)}+\dfrac{z}{\left(z+x\right)+\left(z+y\right)}\le\dfrac{1}{4}\left(\dfrac{x}{x+y}+\dfrac{x}{x+z}\right)+\dfrac{1}{4}\left(\dfrac{y}{y+z}+\dfrac{y}{y+x}\right)+\dfrac{1}{4}\left(\dfrac{z}{z+x}+\dfrac{z}{z+y}\right)=\dfrac{3}{2}\).
Đẳng thức xảy ra khi x = y = x = \(\dfrac{1}{3}\).
Cho x, y là các số thực dương thỏa mãn điều kiện 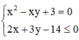 Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức ![]()
A. 12
B. 8
C. 0
D. 4
Đáp án C
Phương pháp:
Rút y theo x từ phương trình (1), thế vào phương trình (2) để tìm khoảng giá trị của x.
Đưa biểu thức P về 1 ẩn x và tìm GTLN, GTNN của biểu thức P.
Cách giải: 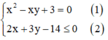
Ta nhận thấy x = 0 không thỏa mãn phương trình (1), do đó 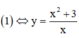 thế vào (2):
thế vào (2):
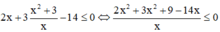
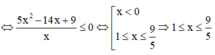
![]()
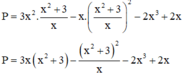
Sử dụng MTCT ta tính được
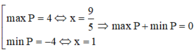
Cho các số thực dương x,y thỏa mãn điều kiện căn(xy)×(x-y)=(x+y)
Tìm Min x+y
cho x,y,z là các số thực dương thỏa mãn điều kiện x+y+z=xyz.Tìm GTNN của biểu thức S=x/y^2 + y/z^2 + z/x^2
M=x+yxy.1z≥2√xyxy.1z=2z√xy≥2z(x+y2)=4z(x+y)M=x+yxy.1z≥2xyxy.1z=2zxy≥2z(x+y2)=4z(x+y)
=4z(1−z)=414−(z−12)2≥16=4z(1−z)=414−(z−12)2≥16
Min M= 16 khi z=1/2 và x=y =1/4