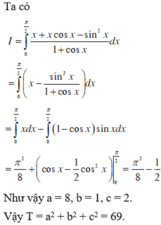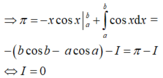Tính tích phân I = ∫ 0 π x 2 cos 2 2 xdx bằng cách đặt u = x 2 d v = cos 2 x dx . Mệnh đề nào dưới đây đúng?
A. I = 1 2 x 2 sin 2 x 0 π - ∫ 0 π x sin 2 xdx
B. I = 1 2 x 2 sin 2 x 0 π - 2 ∫ 0 π x sin 2 xdx
C. I = 1 2 x 2 sin 2 x 0 π + 2 ∫ 0 π x sin 2 xdx
D. I = 1 2 x 2 sin 2 x 0 π + ∫ 0 π x sin 2 xdx