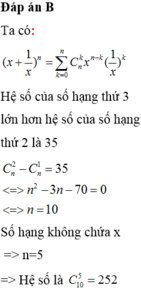tìm số hạng không chứa x trong khai triển (5x-2)10
HP
Những câu hỏi liên quan
a)Tìm số hạng không chứa x trong khai triển (x+2/x)10
b)Tìm số hạng không chứa x trong khai triển (x+2/x2)6
c)Tìm hệ số của số hạng chứa x10 trong khai triển (3x3-2/x2)5
a: SHTQ là: \(C^k_{10}\cdot x^{10-k}\cdot\left(\dfrac{2}{x}\right)^k=C^k_{10}\cdot2^k\cdot x^{10-2k}\)
Số hạng ko chứa x tương ứng với 10-2k=0
=>k=5
=>SH đó là 8064
b: SHTQ là; \(C^k_6\cdot x^{6-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_6\cdot2^k\cdot x^{6-3k}\)
Số hạng ko chứa x tương ứng với 6-3k=0
=>k=2
=>Số hạng đó là 60
c: SHTQ là: \(C^k_5\cdot\left(3x^3\right)^{5-k}\cdot\left(-\dfrac{2}{x^2}\right)^k\)
\(=C^k_5\cdot3^{5-k}\cdot\left(-2\right)^k\cdot x^{15-5k}\)
SH chứa x^10 tương ứng với 15-5k=10
=>k=1
=>Hệ số là -810
Đúng 1
Bình luận (0)
Tìm số hạng không chứa x trong khai triển ( 2x3 + \(\dfrac{1}{x^2}\))10
Số hạng tổng quát trong khai triển:
\(C_{10}^k.\left(2x^3\right)^k.\left(x^{-2}\right)^{10-k}=C_{10}^k.2^k.x^{3k}.x^{2k-20}=C_{10}^k.2^k.x^{5k-20}\)
Số hạng không chứa x \(\Rightarrow5k-20=0\Rightarrow k=4\)
Số hạng đó là: \(C_{10}^4.2^4=...\)
Đúng 1
Bình luận (0)
Trong khai triển nhị thức
x
+
1
x
n
,
x
≠
0
, hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên. A. 225 B. 252 C. 522 D. 525
Đọc tiếp
Trong khai triển nhị thức x + 1 x n , x ≠ 0 , hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức
x
+
1
x
n
,
x
≠
0
hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên. A. 225 B. 252 C. 522 D. 525
Đọc tiếp
Trong khai triển nhị thức x + 1 x n , x ≠ 0 hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Tìm hệ số của số hạng chứa x^10 trong khai triển: (x^2-x^3+1)^10
\(\left(x^2-x^3+1\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(x^2-x^3\right)^k=\sum\limits^{10}_{k=0}C_{10}^k\sum\limits^k_{i=0}C_k^i.\left(x^2\right)^i.\left(-x^3\right)^{k-i}\)
\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^k.C_k^i.\left(-1\right)^{k-i}.x^{3k-i}\)
Số hạng chứa \(x^{10}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le k\le0\\0\le i\le k\\3k-i=10\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(2;4\right);\left(5;5\right)\)
\(\Rightarrow\) Hệ số: \(C_{10}^4.C_4^2+C_{10}^5.C_5^5=...\)
Đúng 0
Bình luận (0)
1. Tìm hệ số của số hạng x^4 trong khai triển left(x-3right)^92. Tìm hệ số của số hạng chứa x^{12}y^{13} trong khai triển left(2x+3yright)^{25}3. Tìm hệ số của số hạng chứa x^4 trong khai triển left(dfrac{x}{3}-dfrac{3}{x}right)^{12}4. Tìm hệ số của số hạng không chứa x trong khai triển left(x^2-dfrac{1}{x}right)^65. Tìm hệ số của số hạng không chứa x trong khai triển left(x+dfrac{1}{x^4}right)^{10}
Đọc tiếp
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
a.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(1+x^2\right)^{12}\)
b.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(2x-1\right)^{10}\)
HELP ME!
Tìm số hạng không chứa x trong khai triển
x
2
-
2
x
15
A
.
2
7
.
C
15
7
B
.
2...
Đọc tiếp
Tìm số hạng không chứa x trong khai triển x 2 - 2 x 15
A . 2 7 . C 15 7
B . 2 10 . C 15 10
C . - 2 10 . C 15 10
D . - 2 7 . C 15 7
Chọn B
Ta có 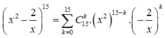
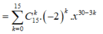
Số hạng không chứa x tương ứng với 30 - 3k = 0 => k = 10
Khi đó số hạng cần tìm là 2 10 . C 15 10 .
Đúng 0
Bình luận (0)