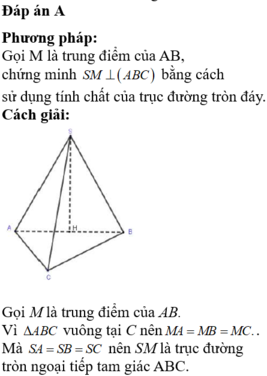
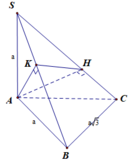
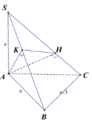
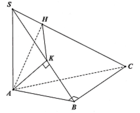
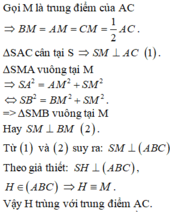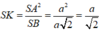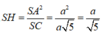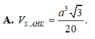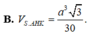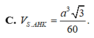Cho hình chóp S.ABC có SA=SB=SC và tam giác ABC vuông tại B Vẽ S H ⊥ A B C , H ∈ A B C . Khẳng định nào sau đây đúng?
A. H trùng với trực tâm tam giác ABC
B. H trùng với trọng tâm tam giác ABC
C. H trùng với trung điểm của AC
D. H trùng với trung điểm BC