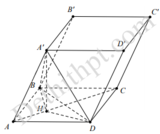
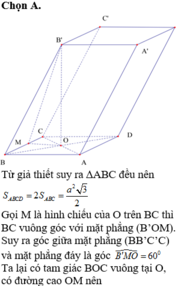
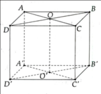
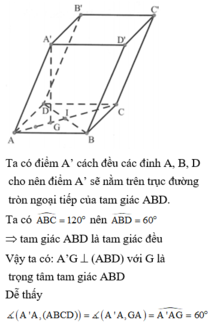
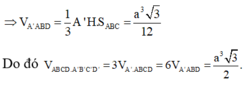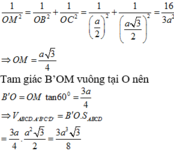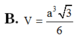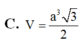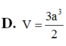Cho hình lăng trụ A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi cạnh a, tâm O và A B C ^ = 120 ° . Các cạnh AA, A'B, A'D cùng tạo với mặt đáy một góc bằng 60 ° . Tính theo a thể tích V của khối lăng trụ đã cho
A. V = a 3 3
B. V = a 3 3 6
C. V = a 3 3 2
D. V = 3 a 3 2