Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
PB
Cho hình hộp A B C D . A B C D  có đáy là hình thoi cạnh a, A B C ^ 60 °  và thể tích bằng 3 a 3  Tính chiều cao h của hình hộp đã cho. A. h 2a B. h a C. h 3a D. h 4a
Đọc tiếp
Lớp 0 Toán
Những câu hỏi liên quan
PB
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là A. S xq 13 πa 2 4 B.  S xq...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
CT
17 tháng 5 2018 lúc 15:56

Bình luận (0)
NA
cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a góc abc=60• .SA vuông góc với mặt phẳng đáy. Tính: a) d(A; (SBD)) b) d(C; (SAB))
Xem chi tiết
Lớp 11 Toán Chương 3: VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓ...

Khách
 
NL
5 tháng 2 2021 lúc 1:27

Đề thiếu dữ liệu để xác định độ dài SA rồi bạn

Bình luận (0)
PB
Hình hộp đứng ABCD.A′B′C′D′ có đáy là hình thoi. Diện tích các tứ giác ABCD,ACC′A′,BDD′B′ lần lượt là S 1 , S 2 , S 3 .  Khi đó thể tích khối hộp ABCD.A′B′C′D′ là A. 1 3 S 1 S 2...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
CT
15 tháng 11 2019 lúc 10:45

Bình luận (0)
H24

Cho hình hộp đứng \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = 2a\) và đáy \(ABCD\) là hình thoi có \(AB = a\) và \(AC = a\sqrt 3 \).

a) Tính khoảng cách giữa hai đường thẳng \(B{\rm{D}}\) và \(AA'\).

b) Tính thể tích của khối hộp.

Xem chi tiết
Lớp 11 Toán Bài 4. Khoảng cách trong không gian

Khách
 
KT
22 tháng 9 2023 lúc 15:18

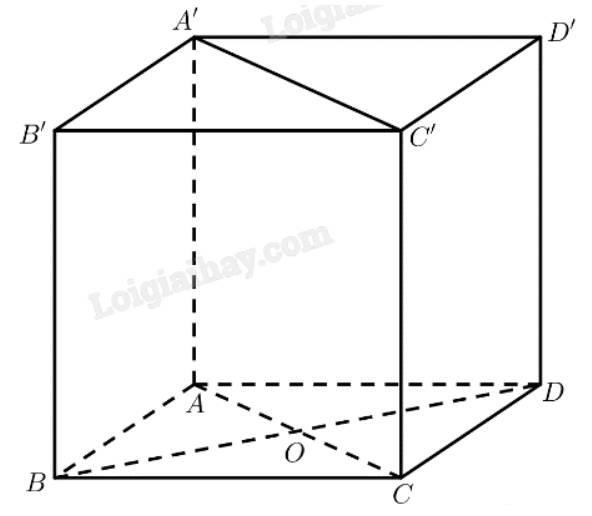
a) Gọi \(O = AC \cap B{\rm{D}}\)

\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)

\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)

\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)

b) Tam giác \(OAB\) vuông tại \(O\)

\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}}  = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)

Bình luận (0)
LT
Câu 2. Cho hình hộp thoi ABCD.ABCD có tất cả các cạnh bằng a và các góc ABC  BBA BBC 60o. Chứng minh tứ giác ABCD là hình vuông. Câu 3. Cho hình hộp ABCD.ABCD có độ dài tất cả các cạnh bằng a và các góc BAD, DAA , AAB đều bằng 60o . Gọi M, N lần lượt là trung điểm của AA , CD. Gọi α là góc tạo bởi hai đường thẳng MN và BC. Tính cos αCâu 4. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a; SA vuông góc với đáy và SA a√3. Khi đó, cosin góc giữa SB và AC bằng 
Đọc tiếp
Xem chi tiết
Lớp 11 Toán Bài 6: Ôn tập chương Vecơ trong không gian. Quan h...

Khách
 
H24

Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\).

Xem chi tiết
Lớp 11 Toán Bài 1. Hai đường thẳng vuông góc

Khách
 
BK
21 tháng 8 2023 lúc 18:47

THAM KHẢO:

Bài tập 1 trang 56 Toán 11 tập 2 Chân trời

CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)

CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)

Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)

Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)

Bình luận (0)
NV
Câu 1: Hình hộp chữ nhật có:A. 6 cạnh B. 10 cạnhC. 8 cạnh D. 12 cạnhCâu 2: Hình hộp chữ nhật có:A. 4 mặt B.5 mặtC. 6 mặt D. 8 mặtCâu 3: Tính diện tích mặt đáy của hình hộp chữ nhật hình có chiều dài a, chiều rộng b , chiều cao h ( cùng đơn vị đo) được tính theo công thức:A. S a+bx2 C. S a x bB. (a+b)x2 D. a: bCâu 4: Diện tích xung quanh của hình hộp chữ nhật là diện tích của:A. 2 mặt đáyB. 4 mặt xung quanhC. 2 mặt xung quanhD. 6 mặtCâu 5: Chu vi mặt đáy của hình hộp chữ nhật có chiều dài 1,5dm...
Đọc tiếp
Xem chi tiết
Lớp 5 Toán Câu hỏi của OLM

Khách
 
TV
12 tháng 2 2022 lúc 14:42

Câu 1: Hình hộp chữ nhật có:

A. 6 cạnh B. 10 cạnh

C. 8 cạnh D. 12 cạnh

Câu 2: Hình hộp chữ nhật có:

A. 4 mặt B.5 mặt

C. 6 mặt D. 8 mặt

Câu 3: Tính diện tích mặt đáy của hình hộp chữ nhật hình có chiều dài a, chiều rộng b , chiều cao h ( cùng đơn vị đo) được tính theo công thức:

A. S = a+bx2 C. S = a x b

B. (a+b)x2 D. a: b

Câu 4: Diện tích xung quanh của hình hộp chữ nhật là diện tích của:

A. 2 mặt đáy

B. 4 mặt xung quanh

C. 2 mặt xung quanh

D. 6 mặt

Câu 5: Chu vi mặt đáy của hình hộp chữ nhật có chiều dài 1,5dm, chiều rộng 1,2dm chiều cao 1dm là:

A. 5,4dm B. 2,5dm

C. 2,7dm D. 5 dm

Lời giải chi tiết: Chu vi mặt đáy là:

   (1,5+1,2)×2=5,4(dm)

               Đáp số: 5,4dm

Bình luận (0)
 Khách vãng lai đã xóa
PB
Cho hình hộp đứng ABCD.A B C D có đáy là hình thoi, AC 6a, BD 8a. Chu vi của một đáy bằng 4 lần chiều cao của khối hộp. Thể tích của khối hộp ABCD.A B C D là: A.  240 a 3 B.  120 a 3 C.  40 a 3 D.  80 a 3
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
CT
3 tháng 3 2018 lúc 12:48

Bình luận (0)
HD

cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, SA vuông góc với mặt phẳng đáy, SA=BD=a√3. Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) bằng

A. 60°  B. 30°  C.90°  D.45°

 

Xem chi tiết
Lớp 12 Toán Câu hỏi của OLM

Khách
 
LP
16 tháng 6 2023 lúc 10:14

 Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).

Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A. 

Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A

 

Bình luận (0)
LP
16 tháng 6 2023 lúc 10:15

Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

Bình luận (0)
PB
Cho hình hộp ABCD.ABCD có đáy là hình chữ nhật, hình chiếu của A lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB a, AD 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (ADCB) bằng:A.  2 a 6             B.  2...
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
CT
6 tháng 4 2017 lúc 11:17

Chọn D.

Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.

Bình luận (0)