Giá trị lớn nhất của hàm số y = 6 - 8 x x 2 + 1 trên tập xác định của nó là
A. - 2
B. 2 3
C. 8
D. 10
PB
Những câu hỏi liên quan
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a. y=\(\sqrt{\text{3(1+ sin(x))}}\)-5
b. y= 6 sin(x+8)-5
Tìm giá trị M lớn nhất của hàm số y =-x^2+6x+8
\(=-\left(x^2-6x-8\right)\)
\(=-\left(x^2-6x+9\right)+17\)
\(=-\left(x-3\right)^2+17\le17\forall x\)
Dấu '=' xảy ra khi x=3
Đúng 1
Bình luận (0)
Cho hàm số
f
x
a
x
+
b
c
x
+
d
với
a
,
b
,
c
,
d
∈
R
có đồ thị hàm số yf(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số yf(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng. A. 2 B. 5 C. 4...
Đọc tiếp
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.
A. 2
B. 5
C. 4
D. 6
Cho hàm số y 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x
∈
[−3; 4] A.
max
−
3
;
4
y
4
B.
min
y
−
2
−
3...
Đọc tiếp
Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x ∈ [−3; 4]
A. max − 3 ; 4 y = 4
B. min y = − 2 − 3 ; 4
C. Cả A, B đều đúng
D. Cả A, B đều sai
Cho hàm số y f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng? A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số. B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y f(x).
C. Số M f(
x
0
) trong đó
x
0
∈ D là giá trị lớn nhất của hàm số y f(x) nếu M f(x), ∀x ∈ D D. Nếu tồn tại
x
0
∈ D...
Đọc tiếp
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
Đúng 0
Bình luận (0)
y= {x2-2x-8 khi x≤2
y= {2x-12 khi x>2
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số khi x ϵ [1;-4] . Tính M+m
Cho hàm số Y=x^2-2(m+1/m)x +m (m>0) xác định trên [-1;1]. Giá trị lớn nhất. giá trị nhỏ nhất của hàm số trên [-1;1] lần lượt là y1'y2 thỏa mãn y1+y2=8. khi đó giá trị của m bằng
Cho hai hàm số yf(x),yg(x) có đạo hàm là f(x),g(x) Đồ thị hàm số f(x), g(x) được cho như hinh vẽ dưới đây Biết rằng f(0)-f(6)g(0)-g(6) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x)f(x)-g(x) trên đoạn [0;6] lần lượt là: A. h(6),h(2) B. h(0),h(2) C. h(2),h(6) D. h(2),h(0)
Đọc tiếp
Cho hai hàm số y=f(x),y=g(x) có đạo hàm là f'(x),g'(x) Đồ thị hàm số f'(x), g'(x) được cho như hinh vẽ dưới đây
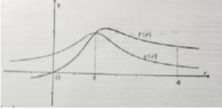
Biết rằng f(0)-f(6)<g(0)-g(6) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [0;6] lần lượt là:
A. h(6),h(2)
B. h(0),h(2)
C. h(2),h(6)
D. h(2),h(0)
Hãy vẽ đồ thị của các hàm số y 2x2, y -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:Nếu a 0 thì hàm số y ax2 đồng biến khi nào? Nghịch biến khi nào?Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?Nếu a 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
Đọc tiếp
Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:
Nếu a > 0 thì hàm số y = ax2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
Vẽ hình:
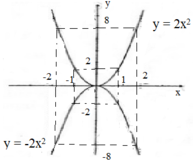
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị lớn nhất của hàm số (nếu có)
a, \(y=\sqrt{x^2+x-2}\)
b, \(y=\sqrt{2+x}+\sqrt{4-x}\)
c, \(y=x+\sqrt{4-x^2}\)
Lời giải:
a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)
Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.
$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học
$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)
Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$
$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky
$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$
Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$
c. ĐKXĐ: $-2\leq x\leq 2$
$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky
$\Leftrightarrow y^2\leq 8$
$\Leftrightarrow y\leq 2\sqrt{2}$
Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$
Mặt khác:
$x\geq -2$
$\sqrt{4-x^2}\geq 0$
$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$
Đúng 1
Bình luận (0)