Cho x, y là hai số thực dương thỏa mãn log 3 2 x + y + 1 x + y = x + 2 y .Tìm giá trị nhỏ nhất của biểu thức P = 1 x + 2 y ,
A. 3 + 3
B. 3 + 2 3
C. 6
D. 4
Cho x,y là các số thực dương thỏa mãn \(x+y\le1\)
CMR \(\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy\ge11\)
\(VT=\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\left(\frac{1}{4xy}+4xy\right)+\frac{5}{4xy}\)
\(\ge\frac{4}{\left(x+y\right)^2}+2+\frac{5}{\left(x+y\right)^2}\ge4+2+5=11\)
Tìm hai số thực x và y thỏa mãn (3x+2yi)+(3-i)=4x-3i với i là đơn vị ảo.
A. ![]()
![]() .
.
B. ![]()
![]() .
.
C. ![]()
![]() .
.
D. ![]()
![]() .
.
Bài 1:Cho a,b là các số nguyên tố thỏa mãn: (a-1) chia hết cho b và (b3 - 1) chia hết cho a.Chứng minh: a= b2+b+1
Bài 2:Cho x,y là hai số thực thỏa mãn:
x3 + y3 +3x2 + 4x + 3y2 +4y +4=0.Tìm giá trị lớn nhất của biểu thức P=1/x+1/y
1) Vì a, b là số nguyên tố và a - 1 chia hết cho b nên a là số nguyên tố lẻ >=3 và b =2( vì a -1 chẵn)
b3 - 1 = 7 chia hết cho a, nên a =7. Vậy a = b2 + b + 1( 7 = 22 + 2 + 1)
Cho các số thực x, y thỏa mãn x + y = 2 x - 3 + y + 3 . Giá trị nhỏ nhất của biểu thức P = 4 ( x 2 + y 2 ) + 15 x y là:
A. minP = -83
B. minP = -63
C. minP = -80
D. minP = -91
Các số thực x, y thỏa mãn đẳng thức x(3 + 5i) - y(1 + 2i) = 9 + 16i . Giá trị biểu thức T = |x - y| là
A. 0
B. 1
C. 3
D. 5
Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
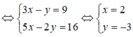
Vậy: T = |x - y| = 5
cho x,y là 2 số thực thỏa mãn x>y ,xy=1
Cmr: (x^2+y^2)^2 / (x-y)^2 >= 8
giả sử x,y là những số thực dương phân biệt thỏa mãn:
\(\frac{y}{x+y}+\frac{2y^2}{x^2+y^2}+\frac{4y^4}{x^4+y^4}+\frac{8y^8}{x^8-y^8}=4\)
CMR: 5y=4x
giúp em câu này ạ
cho x,y là các số thực thỏa mãn
căn(2x+3) +căn(y+3) =4
tìm min p=căn(x+2 )+căn(y+9)
Cho x,y là các số thực dương thỏa mãn:2y>x.CMR:\(\frac{1}{x^3\left(2y-x\right)}+x^2+y^2\)≥3
\(P=\frac{1}{x^3\left(2y-x\right)}+x\left(2y-x\right)-x\left(2y-x\right)+x^2+y^2\)
\(P\ge\frac{2}{x}-2xy+2x^2+y^2\)
\(P\ge\frac{1}{x}+\frac{1}{x}+x^2+\left(x-y\right)^2\ge3+\left(x-y\right)^2\ge3\)
Dấu "=" xảy ra khi \(x=y=1\)
Lời giải:
Với $x,y$ là các số thực dương, áp dụng BĐT Cauchy ta có:
\(x^2+y^2\geq 2xy\)
\(\Rightarrow \frac{1}{x^3(2y-x)}+x^2+y^2\geq \frac{1}{x^3(2y-x)}+2xy(1)\)
$2y>x$ nên $2y-x>0$. Tiếp tục áp dụng BĐT Cauchy cho các số dương ta có:
\(\frac{1}{x^3(2y-x)}+2xy=\frac{1}{x^3(2y-x)}+x(2y-x)+x^2\geq 3\sqrt[3]{\frac{1}{x^3(2y-x)}.x(2y-x).x^2}=3(2)\)
Từ \((1);(2)\Rightarrow \frac{1}{x^3(2y-x)}+x^2+y^2\geq 3\) (đpcm)
Dấu "=" xảy ra khi $x=y=1$