a. 2cos2x – 3cosx + 1 = 0
Giải phương trình sau: 2cos2x – 3cosx + 1 = 0
2cos2x – 3cosx + 1 = 0 (Phương trình bậc hai với ẩn cos x).
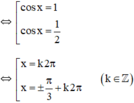
Vậy phương trình có tập nghiệm
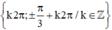
Giá trị lớn nhất của hàm số y = 1 3 c o s 3 x - 2 c o s 2 x + 3 c o s x + 1 , x thuộc 0 ; π 2
A. 1
B. 7 3
C. 2
D. 1 3
 8cos(x-pi/3)^3-3cosx-3căn3sinx+2cos2x=0
8cos(x-pi/3)^3-3cosx-3căn3sinx+2cos2x=0
Giúp mình bài này với ạ cảm ơn mng nhiều
Gpt : Sin2x-2Cos2x-Sinx+3Cosx-1=0
Giải các pt
a) \(\frac{2cosx-1}{2cosx+1}=3\)
b) \(cosx\left(2cos2x-1\right)=3cosx\)
c) \(sin2x.cos2x=0\)
a/ ĐKXĐ: \(cosx\ne-\frac{1}{2}\)
\(\Leftrightarrow2cosx-1=6cosx+3\)
\(\Leftrightarrow4cosx=-4\Rightarrow cosx=-1\)
\(\Rightarrow x=\pi+k2\pi\)
b/
\(\Leftrightarrow cosx\left(2cos2x-1\right)-3cosx=0\)
\(\Leftrightarrow cosx\left(2cos2x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cos2x=2\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=\frac{\pi}{2}+k\pi\)
c/
\(\Leftrightarrow2sin2x.cos2x=0\)
\(\Leftrightarrow sin4x=0\)
\(\Rightarrow4x=k\pi\Rightarrow x=\frac{k\pi}{4}\)
Ptrinh \(\left(2cos2x-1\right)\left(3cosx+1\right)=0\) có bao nhiêu nghiệm thuộc khoảng \(\left(-\frac{\pi}{4};\frac{\pi}{2}\right)\)
Với \(x\in\left(-\frac{\pi}{4};\frac{\pi}{2}\right)\Rightarrow cosx>0\Rightarrow3cosx+1>0\)
Do đó pt tương đương:
\(2cos2x-1=0\Rightarrow cos2x=\frac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\frac{\pi}{3}+k2\pi\\2x=-\frac{\pi}{3}+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k\pi\\x=-\frac{\pi}{6}+k\pi\end{matrix}\right.\)
Pt có 2 nghiệm thuộc khoảng đã cho là \(x=\left\{-\frac{\pi}{6};\frac{\pi}{6}\right\}\)
A, sin2 x- 4sinx +3=0
B, 2cos2x- cosx-1=0
C, 3sin2x- 2cosx +2=0
D, 3cosx+ cos2x -cos3x +1=2sinx.sin2x
E, tan2 x+(\(\sqrt{3}\) +1)tanx-\(\sqrt{3}\)=0
F, \(\dfrac{\sqrt{3}}{sin^2x}\)=3cotx + \(\sqrt{3}\)
a, \(sin^2x-4sinx+3=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow sinx=1\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
b, \(2cos^2-cosx-1=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
c, \(3sin^2x-2cosx+2=0\)
\(\Leftrightarrow3-3sin^2x+2cosx-5=0\)
\(\Leftrightarrow3cos^2x+2cosx-5=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(3cosx+5\right)=0\)
\(\Leftrightarrow cosx=1\)
\(\Leftrightarrow x=k2\pi\)
Giải pt sau :
1/ (2sinx-1)(2cos2x+2sinx+1)=3-4cos2 x
2/ \(\sqrt{3}cot\left(\frac{\pi}{4}-x\right)+1=0\)
3/ (cos\(\frac{x}{4}-3sinx\)) sinx + (\(\left(1+sin\frac{x}{4}-3cosx\right)cosx=0\)
4/ \(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(\left(2sinx-1\right)\left(2cos2x+2sinx+1\right)=3-4\left(1-sin^2x\right)\)
\(\Leftrightarrow\left(2sinx-1\right)\left(2cos2x+2sinx+1\right)=4sin^2x-1\)
\(\Leftrightarrow\left(2sinx-1\right)\left(2cos2x+2sinx+1\right)-\left(2sinx-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(2cos2x+2sinx+1-2sinx-1\right)=0\)
\(\Leftrightarrow2cos2x\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sinx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
2.
ĐKXĐ: ...
\(\Leftrightarrow cot\left(\frac{\pi}{4}-x\right)=-\frac{1}{\sqrt{3}}\)
\(\Leftrightarrow\frac{\pi}{4}-x=-\frac{\pi}{3}+k\pi\)
\(\Leftrightarrow x=\frac{7\pi}{12}+k\pi\)
3.
\(\Leftrightarrow cos\frac{x}{4}sinx+sin\frac{x}{4}.cosx-3\left(sin^2x+cos^2x\right)+cosx=0\)
\(\Leftrightarrow sin\left(x+\frac{x}{4}\right)=-cosx\)
\(\Leftrightarrow sin\frac{5x}{4}=sin\left(x-\frac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{5x}{4}=x-\frac{\pi}{2}+k2\pi\\\frac{5x}{4}=\frac{3\pi}{2}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
4.
\(\Leftrightarrow2sinx.cosx-\left(1-2sin^2x\right)+3sinx-cosx-1=0\)
\(\Leftrightarrow cosx\left(2sinx-1\right)+2sin^2x+3sinx-2=0\)
\(\Leftrightarrow cosx\left(2sinx-1\right)+\left(2sinx-1\right)\left(sinx+2\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2sinx-1=0\\sinx+cosx=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\sin\left(x+\frac{\pi}{4}\right)=-\sqrt{2}< -1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)
HELPING NOW!!!
Giair phương trình lượng giác sau:
1) cosx - cos2x +cos3x = 0
2) cos2x - sin2x = sin3x + cos4x
3) cos2x + 2sinx - 1 - 2sinxsosx = 0
4) 1+ sinx - cosx = sin2x - cos2x
5) \(\sqrt{2}\) sin (2x+\(\dfrac{\pi}{4}\)) - sinx - 3cosx +2 =0
6) sin2x + 2cos2x = 1+sinx - 4cosx