Có bao nhiêu số thực m để tôn tại duy nhất cặp số thực (x;y) thỏa mãn đồng thời log x 2 + y 2 + 2 4 x + 4 y + m 2 - m - 5 ≥ 1 và x 2 + y 2 + 2 x - 4 x + 1 = 0 .
A. 2.
B. 6.
C. 4.
D. 0.
PB
Những câu hỏi liên quan
Có bao nhiêu giá trị thực của tham số m để phương trình
9
x
+
9
m
.
3
x
.
cosπ
x
có duy nhất 1 nghiệm thực A. 1 B. 0 C. 2 D. vô số
Đọc tiếp
Có bao nhiêu giá trị thực của tham số m để phương trình 9 x + 9 = m . 3 x . cosπ x có duy nhất 1 nghiệm thực
A. 1
B. 0
C. 2
D. vô số
Có bao nhiêu giá trị thực của tham số m để phương trình 9 x + 9 = m 3 x c o s π x có duy nhất 1 nghiệm thực
A. 1
B. 0
C. 2
D. Vô số
Có bao nhiêu giá trị thực của tham số m để phương trình 9 x + 9 = m 3 x cosπ x có duy nhất 1 nghiệm thực.
A. 1
B. 0
C. 2
D. Vô số
Chọn A.
Phương pháp: Đặt ẩn phụ không hoàn toàn.
Cách giải: Ta có:
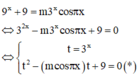
Điều kiện cần để phương trình đã cho có nghiệm duy nhất là (*) phải có đúng nghiệm dương
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
2
x
+
2
y
+
5
≥
1
, giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho...
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ 1 , giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x 2 + y 2 + 4 x + 6 y + 13 - m = 0 thuộc tập nào sau đây?
A. [8;10]
B. [5;7]
C. [1;4]
D. [-3;0]
Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
(
2
x
+
2
y
+
5
)
≥
1
giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m 0 thuộc tập nào sau đây?
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 ( 2 x + 2 y + 5 ) ≥ 1 giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m = 0 thuộc tập nào sau đây?
Đáp án A
Ta có, giả thiết
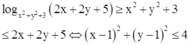
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và
Đúng 0
Bình luận (0)
Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
6
+
m...
Đọc tiếp
Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 6 + m 2 ≥ 1 và x 2 + y 2 + 2 x - 4 y + 1 = 0 .
A. S = - 5 ; 5
B. S = - 7 ; - 5 ; - 1 ; 5 ; 7
C. S = - 5 ; - 1 ; 1 ; 5
D. S = - 1 ; 1
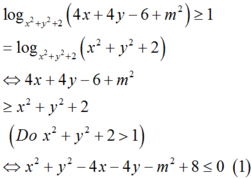
Ta có
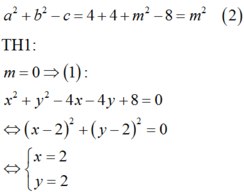
Cặp số x ; y = 2 ; 2 không thỏa mãn điều kiện .
Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .
Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2 bán kính R 2 = 1 + 4 - 1 = 2 .
Để tồn tại duy nhất cặp số (x;y) thỏa mãn 2 điều kiện (1) và (2) Xảy ra 2 trường hợp sau:
TH1: C1; C2tiếp xúc ngoài
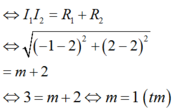
TH2: C1; C2 tiếp xúc trong và
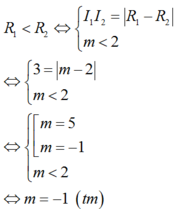
Vậy S = - 1 ; 1 .
Chọn D.
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên
a
∈
-
200
;
200
để phương trình
e
x
+
e
x
+
a
ln
1
+
x
-
ln
x
+
a...
Đọc tiếp
Có bao nhiêu số nguyên a ∈ - 200 ; 200 để phương trình e x + e x + a = ln 1 + x - ln x + a + 1 có nghiệm thực duy nhất.
A. 399
B. 199
C. 200
D. 398
Có bao nhiêu số nguyên
a
∈
(
-
200
;
200
)
để phương trình
e
x
+
e
x
+
a
ln
(
1
+
x
)
-
ln
(
x
+
a...
Đọc tiếp
Có bao nhiêu số nguyên a ∈ ( - 200 ; 200 ) để phương trình e x + e x + a = ln ( 1 + x ) - ln ( x + a + 1 ) có nghiệm thực duy nhất.
A. 399
B. 199
C. 200
D. 398
Cho hàm số
y
f
(
x
)
thỏa mãn
lim
x
→
-
∞
f
(
x
)
2019
m
,
lim
x
→
+
∞
f
(
x
)
2020
m
4...
Đọc tiếp
Cho hàm số y = f ( x ) thỏa mãn lim x → - ∞ f ( x ) = 2019 m , lim x → + ∞ f ( x ) = 2020 m 4 (với m là tham số thực). Hỏi có tất cả bao nhiêu giá trị của m để đồ thị của hàm số y = f ( x ) có duy nhất một tiệm cận ngang?
A. 4
B. 2
C. 3
D. 1
