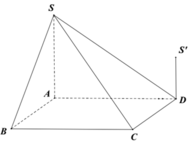
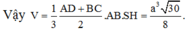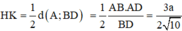Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SASBSCSDa√2; O là tâm của hình vuông ABCD.a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD). b) C/m (SAC) ⊥(SBD)c) Tính khoảg cách từ S đến (ABCD)d) Tính góc giữa đường SB và (ABCD).e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCDf) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)g) Tính khoảng cách giữa SM và BC; SM và AB.
Đọc tiếp
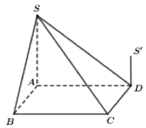
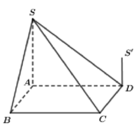
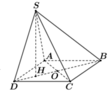
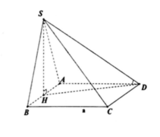
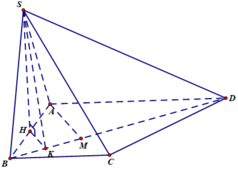
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.