Cho tứ diện ABCD có AB = 3, AC = 2, AD = 6, B A C ^ = 90 ° , C A D ^ = 120 ° , B A D ^ = 60 ° . Thể tích khối tứ diện ABCD bằng
A. 6 2
B. 2 2 3
C. 2
D. 3 2
PB
Những câu hỏi liên quan
Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)
Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)
\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)
\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)
Đúng 1
Bình luận (0)
Cho tứ diện ABCD có
A
B
a
,
A
C
2
,
A
D
3
,
B
A
C
^
C
A
D
^
D
A
B
^...
Đọc tiếp
Cho tứ diện ABCD có A B = a , A C = 2 , A D = 3 , B A C ^ = C A D ^ = D A B ^ = 90 ° . Khoảng cách từ A đến mặt phẳng (BCD) là
A. 6 7
B. 6 13 13
C. 2 5 5
D. 6 10 10
Chọn A
Gọi P là hình chiếu vuông góc của A trên cạnh BC và H là hình chiếu vuông góc của A trên DP.
Khi đó d ( A , ( B C D ) ) = A H = 6 7
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
B
,
A
C
,
A
D
đôi một vuông góc với nhau,
A
B
a
,
A
C
b
,
A
D
c
.
Tính thể tích V của khối tứ diện ABCD theo a, b, c A.
V
a
b
c
2...
Đọc tiếp
Cho tứ diện ABCD có A B , A C , A D đôi một vuông góc với nhau, A B = a , A C = b , A D = c . Tính thể tích V của khối tứ diện ABCD theo a, b, c
A. V = a b c 2
B. V = a b c 6
C. V = a b c 3
D. V = a b c
Đáp án B
V A . B C D = 1 3 A D . S A B C = 1 6 A B . A C . A D = a b c 6
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, ABa, ACb, ADc Tính thể tích V của khối tứ diện ABCD theo a, b, c
Đọc tiếp
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, AB=a, AC=b, AD=c Tính thể tích V của khối tứ diện ABCD theo a, b, c
Cho tứ diện ABCD có AB 3, AC 2, AD 6, BAC 900, CAD 1200, BAD 600 . Thể tích khối tứ diện ABCD bằng A. 6
2
B.
2
2
3
C.
2
D. 3
2
Đọc tiếp
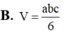
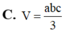
Cho tứ diện ABCD có AB = 3, AC = 2, AD = 6, BAC = 900, CAD = 1200, BAD = 600 . Thể tích khối tứ diện ABCD bằng
A. 6 2
B. 2 2 3
C. 2
D. 3 2
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
Cách giải:
Áp dụng công thức 
ta được: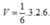
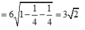
Chọn D.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB a; AC a
2
; AD a
3
,(a0) Thể tích V của khối tứ diện ABCD là: A.
V
a
3
6
3
B. ...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Đáp án B
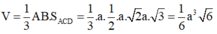
Phương án nhiễu.
A. Sai vì 2 cách: một là thấy số 1 3 cứ chọn, hai là trong công thức thể tích thiếu 1 3 diện tích đáy.
C. Sai vì thiếu 1 3 trong công thức thể tích.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB1, AC2, AD3,
B
A
C
^
C
A
D
^
D
A
B
^
90
°
. Côsin của góc giữa hai mặt phẳng (ABC) và (BCD) là A.
2
7
B. ...
Đọc tiếp
Cho tứ diện ABCD có AB=1, AC=2, AD=3, B A C ^ = C A D ^ = D A B ^ = 90 ° . Côsin của góc giữa hai mặt phẳng (ABC) và (BCD) là
A. 2 7
B. 2 13 13
C. 3 5 7
D. 1 3
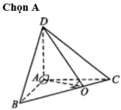
Gọi O là hình chiếu vuông góc của A lên cạnh BC. Khi đó góc giữa hai mặt phẳng (ABC) và (BCD) là
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có ABCD3, ADBC5, ACBD6. Tính thể tích khối cầu ngoại tiếp tứ diện ABCD.
Đọc tiếp
Cho tứ diện ABCD có AB=CD=3, AD=BC=5, AC=BD=6. Tính thể tích khối cầu ngoại tiếp tứ diện ABCD.
